Уравнение теплопроводности

В этом параграфе будут рассмотрены элементы математической теории теплопроводности. Основы этой теории были заложены французским математиком Фурье (1768-1830) в первой четверти XIX века. Естест­венно, что Фурье исходил из представлений теории теплорода, которой тогда пытались объяснить все тепловые явления. Эти представления не­верны. Но если объем системы или давление поддерживаются постоянными, то явления протекают так, как если бы теплота была каким-то веществом, которое может только перемещаться в пространстве, но не может создаваться или уничтожаться. Если постоянен объем системы, то количество теплоты следует отождествить с внут­ренней энергией, а если постоянно давление, то — с энтальпией системы. В обоих случаях математические основы теории теплопроводности Фурье остаются верными, хотя их физическое обоснование не имеет ничего общего с представлениями, из которых исходил сам Фурье.

В дальнейшем предполагается, что передача теплоты осуществляется исключительно путем теплообмена. Предполагается, что конвекции нет. В твердых телах это осуществляется само собой. В жидкостях же и газах надо позаботиться, чтобы конвекция была устранена, например, нагре­вать эти тела сверху. Точно так же предполагается, что потерями теплоты на лучеиспускание можно пренебречь. Кроме того, будем предполагать, что объем системы остается постоянным, так что никаких переме­щений вещества в процессе передачи теплоты не возникает. Ограничимся, наконец, рассмотрением только одномерных задач, когда температура тела, помимо времени, зависит только от одной пространственной ко­ординаты.

В математической теории теплопроводности распространение теплоты рассматривается подобно течению жидкости. Плотностью потока теп­лоты называется вектор j, совпадающий по направлению с направлением распространения теплоты и численно равный количеству теплоты, прохо­дящему в одну секунду через площадку в один квадратный сантиметр, перпендикулярную к направлению потока теплоты. Найдем дифференциальное уравнение, которому удовлетворяет вектор j в одномерных задачах.

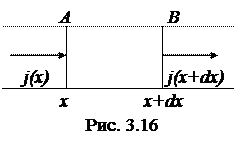Пусть имеется неограниченная среда, в которой возникает поток теплоты в направлении, параллельном оси X. В одномерном общем случае свойства среды и величины, характеризующие тепловой поток, могут меняться в том же направлении. Кроме того, они могут меняться во времени. Поэтому плотность потока теплоты j следует рассматривать как функцию координаты x и времени t: j = (x, t). Выделим мысленно в среде бесконечно

длинную призму или цилиндр с образующими, параллельными оси X, и рассмотрим бесконечно малый участок такого цилиндра АВ длиной dx (рис. 3.16). Пусть S — площадь поперечного сечения цилиндра. Количество теплоты, поступающее в цилиндр АВ за время dt через основание А с координатой x, равно j (x)Sdt. Количество теплоты, уходящее за то же время через основание В, будет j (x + dx)Sdt. Так как через боковую поверхность цилиндра теплота не поступает, то полное количество теплоты, поступающее за время dt через рассматриваемый участок цилиндра, равно

.

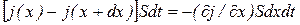Но эту теплоту можно представить в виде dM × c_vdT, где dM = ρ Sdx - масса цилиндра АВ, c_v — удельная теплоемкость, dТ — повышение температуры. Приравнивая оба выражения и производя сокращение, получим

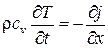. (3.35)

Теперь надо установить связь между плотностью потока теплоты и температурой среды Т. Опыт показывает, что поток теплоты имеет место только тогда, когда температура среды меняется от точки к точке. Теплота течет всегда в направлении от высшей температуры к низшей. Простейшим является случай бесконечной однородной пластинки толщиной l. Если на одной плоской границе пластинки поддерживается температура T₁,а на другой - температура Т₂, причем Т₁ > Т₂, то опыт показывает, что поток теплоты пропорционален разности температур Т₁ –Т₂ и обратно пропорционален толщине пластинки l. Математически это можно представить в виде

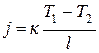, (3.36)

где к — положительная постоянная, зависящая только от материала пла­стинки и его физического состояния. Эта постоянная называется тепло­проводностью материала пластинки. Термин «теплопроводность» употребляется в двух смыслах: 1) как явление передачи теплоты, 2) как коэффициент для количественного описания этого яв­ления. Из контекста будет ясно, в каком смысле употребляется этот термин. Ана­логичное замечание по терминологии относится и к другим понятиям, как-то: температуропроводностъ, диффузия, термодиффузия, вязкость, поверхностное натя­жение и пр. Впрочем, перед некоторыми аналогичными понятиями слово «коэф­фициент» необходимо сохранить. Примером может служить коэффициент концент­рации диффузии.

Допустим, что пластинка бесконечно тонкая. Если ось X направлена в сторону понижения температуры, то l = dx, T₁ = T(x), T₂ = T(x+dx),

,

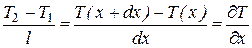и формула (3.35) переходит в

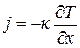. (3.37)

Выражение (3.37) остается верным и в том случае, когда ось X направлена в сторону повышения температуры, так как в этом случае l = - dx, T₁ = Т(х + dx), Т₂ = Т(х). Оно также справедливо и в общем случае не­однородной среды с совершенно произвольным распределением темпе­ратуры, и притом не только слоистой среды, но и такой, свойства и тем­пература которой являются функциями всех трех пространственных коор­динат х, у, z. Достаточно в рассматриваемой точке пространства направить ось X в сторону максимального понижения или повышения температуры и рассмотреть бесконечно тонкий слой, перпендикулярный к этому на­правлению. Такой слой может считаться однородным, и к нему приме­нима формула (8.3). Теплопроводность к будет функцией всех трех пространственных координат х, у, z. В нашей одномерной задаче она бу­дет зависеть только от одной пространственной координаты х: к = к(х).

Если выражение (3.37) подставить в формулу (3.35), то получится

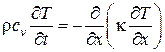. (3.38)

Это уравнение называется уравнением теплопроводности. В частном случае, когда среда однородна и теплопроводность к не зависит от температуры, уравнение принимает вид:

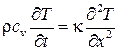, (3.39)

или

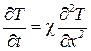, (3.40)

где введено обозначение

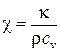. (3.41)

Постоянная χ называется температуропроводностью среды.

В среде могут оказаться источники теплоты. Например, теплота может выделяться в результате прохождения электрического тока или радиоактивного распада. Такие источники мы не принимали во внимание. Чтобы их учесть, введем величину q, равную количеству теплоты, выделяемому источниками в единице объема среды в одну секунду. Тогда вместо уравнения (3.35) следует писать

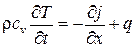. (3.42)

В соответствии с этим изменятся и остальные уравнения.

В общем случае, когда свойства и температура среды зависят от всех трех пространственных координат х, у, z, уравнение теплопровод­ности, выражающее баланс теплоты в теле, имеет вид:

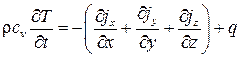. (3.43)

Однако решения такого уравнения аналитически можно получить только в простейших случаях. Наиболее важными являются случаи, когда среда и распределение температуры в ней обладают сферической или цилиндрической симметрией. Поэтому мыне будем использовать уравнение (8.9) в общем виде, а ограничимся случаями сферической и цилиндрической симметрии. В этих случаях вместо прямоугольной системы координат более удобными являются сферическая и цилиндрическая координатные системы.

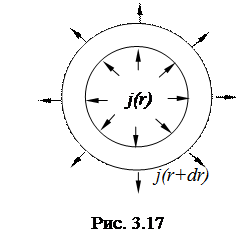Рассмотрим сначала случай сферической симметрии. Вектор плотности потока теплоты j направлен вдоль радиуса, причем j, помимо времени зависит только от r. Опишем вокруг центра симметрии две концентрические сферы с радиусами r и r + dr (рис. 3.17). Количество теплоты, по­ступающее за время dt в пространство между этими сферами через первую их них, равно j(r) × 4 π r²dt. Количество теплоты, вытекающее за то же время через вторую сферу, будет j (r + dr) × 4 π (r + dr)²dt. Эти два ко­личества удобно писать в виде 4 π (jr²)_rdt и 4 π (jr²)_r+drdt, чтобы подчеркнуть, что речь идет об одной и той же функции jr ², но при разных значениях аргумента: r и r + dr. Разность между ними

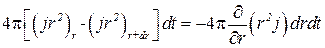
даёт количество теплоты, втекающее за время dt в рассматриваемый сферический слой из окружающего пространства. При наличии источников сюда надо добавить количество теплоты 4 π qr²drdt, поставляемое источниками в сферическом слое. Но изменение количества теплоты в слое можно представить в виде ρ • 4πr²dr • c_vdT. Поэтому уравнение баланса теплоты будет

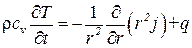. (3.44)

Вместо соотношения (3.37) следует писать j = -к ∂ T/ ∂ r, так что

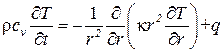. (3.45)