Броуновское движение. Уравнение Ланжевена

В основе этого явления лежит воздействие на систему случайной силы. Частный случай такого движения был описан Г. Броуном в 1827 г. Однако характер этого движения был понят только в XX веке.

Рассмотрим движение крупных частиц в термически однородной среде типа газа или жидкости. Термин «крупные частицы» в данном случае означает, что частицы макроскопически наблюдаемы, т.е. размер их порядка R ~ 10^-4 см (для зеленого света l ~ 0.5×10^-4 см). Этот размер и с молекулярной точки зрения является большим.

Например, для воздуха при нормальных условиях среднее расстояние между молекулами ~ 0.5×10^-7 см, для жидкости – на порядок меньше.

Будем считать, что известны форма, размер, масса и т.д. броуновской частицы (БЧ), а также все свойства среды.

Рассмотрим облака БЧ, полагаем, что они не взаимодействуют друг с другом. Поэтому мы вправе рассматривать какую-либо одну БЧ.

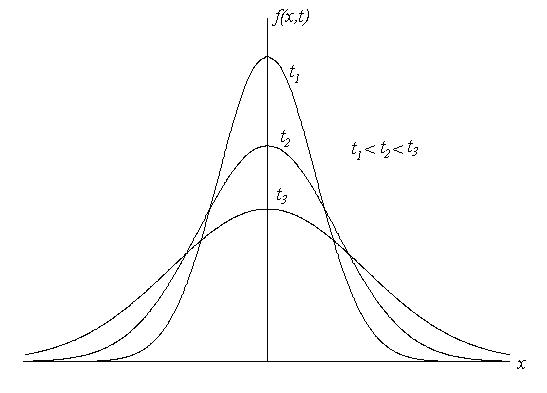
Такая крупная частица взаимодействует сразу с большим числом частиц среды и под действием общей равнодействующей совершает два типа случайных блужданий (рис.3.22):

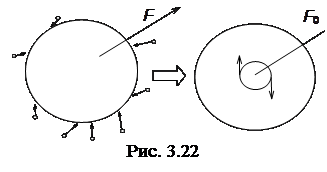а) флуктуации общей величины приводят к трансляционному броуновскому движению,

б) флуктуации момента равнодействующей силы – к вращательному броуновскому движению.

Математически эти процессы во многом эквивалентны, а значит, ограничимся первым типом.

Рассмотрим пространственно однородную систему (потенциал внешней силы 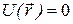) и в ней – одну БЧ. Т.к. направления x, y, z эквивалентны, исследуем одномерное броуновское движение вдоль оси x.

Выделим из силы F, действующей на БЧ, ту ее часть, которая существовала бы и в отсутствие флуктуаций. Эта регулярная часть силы F представляет собой не что иное, как силу вязкого трения (которая нам известна).

Например, для сферических частиц радиуса R согласно формуле Стокса:

,

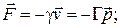
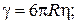
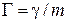h - коэффициент вязкости; v, p – скорость и импульс.

Тогда точное уравнение движения БЧ можно записать в виде:

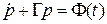
- уравнение Ланжевена (1908 г.),

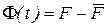- случайная часть силы, действующей на БЧ. В среднем она равна нулю:

<F(t)> = 0.

Проанализируем временные интервалы взаимодействия БЧ с окружением:

– время соударения частицы с частицей среды t ~ 10^-12 c
(для R ~ 10^-4 см);

– время между отдельными взаимодействиями t ' ~ 10^-16 ¸ 10^-17 c;

– время исчезновения информации (релаксации) о начальном состоянии t_М ~ G^{- 1} ~ 10^-10 c.

При сравнении величин этих интервалов обращают на себя внимание характерные соотношения:

t' << tиt << G ^{- 1} .

Уравнение Фоккера-Планка

Теперь рассмотрим трехмерную систему БЧ и будем описывать эволюцию БЧ (или идеального газа БЧ) с помощью функций распределения f в самой грубой временной шкале t >> G^-1.

Распределение по импульсам БЧ в этой шкале является в любой момент времени максвелловским. Поэтому нас будет интересовать только функция распределения по координатам 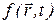, такая, что 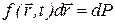- вероятность обнаружить частицу в объеме 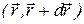, причем

.

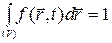Т.к. частицы стабильны (нет их источников), то функция 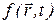должна удовлетворять уравнению непрерывности

.

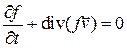Введя грубую шкалу времени (включая dt >> G^-1), t >> G^{- 1}, мы фактически лишим себя возможности использовать микроскопические соображения для превращения этого соотношения в уравнение для одной функции .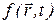

Оставаясь в рамках полуфеноменологического рассмотрения, представим плотность потока 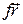как бы складывающуюся из двух частей

.

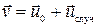Первая из них 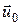обусловлена внешними силами, действующими на БЧ, вторая 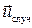- случайными «флуктуирующими» воздействиями на нее со стороны частиц среды.

Для регулярной части используем представления гидродинамики (малые скорости, сферические частицы)

F _внеш. = g u ₀, g = 6p R h,

Поэтому упорядоченный поток частиц можно записать в виде

,

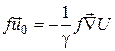где U – потенциал внешнего силового поля.

Случайное же блуждание с макроскопической точки зрения имеет характер диффузионного процесса, поэтому диффузионный поток частиц можно записать (случай малых градиентов)

,

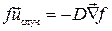где величина D по физическому смыслу является коэффициентом диффузии БЧ данного размера, массы в среде с данной T, h и т.д.

D можно определить экспериментально, но это сложно сделать во всех случаях жизни. В связи с этим рассмотрим предел 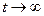, когда система достигнет своего состояния ТД равновесия (нет потоков, все характеристики постоянны). Поэтому помимо df / dt имеем три уравнения для компонент потоков

,

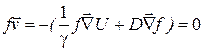которые можно записать в виде

.

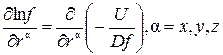Решение этого уравнения

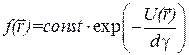
мы могли бы предсказать заранее, т.к. идеальный газ БЧ в поле 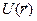характеризуется в равновесном случае больцмановским распределением

, ().

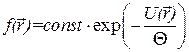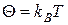Сопоставляя эти выражения, мы получаем, что коэффициент диффузии D просто связан с T, h и R БЧ

.

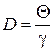Подставляя это выражение в уравнение непрерывности, получим уравнение для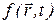

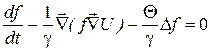. (3.56)

Это и есть уравнение Фоккера-Планка (1914-1917). Дополненное условием нормировки, начальным (НУ) и граничными (ГУ) условиями, оно полностью определяет решение для искомой функции 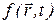. Это решение определяет эволюцию системы на времени t >> G^{- 1}, которая имеет релаксационный характер (к распределению Больцмана) с некоторым временем релаксации t_полн, зависящим уже не только от индивидуальных свойств среды и БЧ, но и от начального распределения, формы и размеров сосуда и т.д.

Рассмотрим случай отсутствия внешнего поля 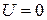и бесконечной одномерной системы с условием отсутствия потоков на бесконечности и НУ, соответствующими нахождению БЧ в точке :

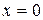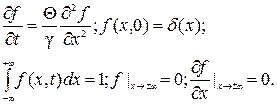(3.57)

Решение уравнения (3.57), удовлетворяющее начальным и граничным условиям, выглядит следующим образом:

.

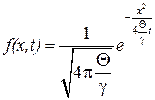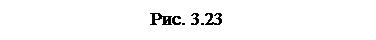
Очевидно, что 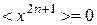- ввиду симметрии функции :

.

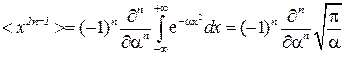В частности, средний квадрат смещения БЧ определяется формулой Эйнштейна

.

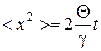Значение полученного решения для 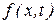не ограничивается только рамками рассмотренного примера. Эта функция может служить основой для получения ряда распределений по другим характеристикам свободного броуновского движения и для проведения оценок.

Оценим время заполнения БЧ сосуда конечных размеров. С математической точки зрения время такой релаксации равно . Речь идет о физической оценке эффективного времени релаксации.

Рассмотрим сначала одномерную систему, в которой движение БЧ ограничено стенками, так что 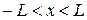. Если бы 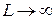, то эффективный размер облака БЧ определялся бы формулой Эйнштейна

.

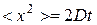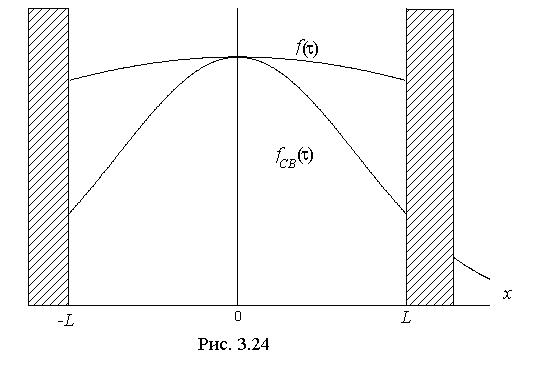
Если бы на расстоянии 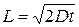от точки 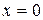по обе стороны стояли стенки, то внутри системы за это время 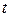мы получили бы достаточно равномерное распределение БЧ. Поэтому и полагают, что время полной релаксации в слое 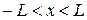имеет величину .

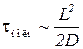В двумерном случае (БЧ в плоской кювете радиусом 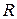) формула Эйнштейна имеет вид:

®

.

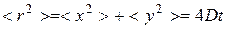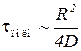Аналогично в трехмерном случае:

,

.

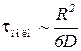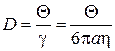Полученная оценка груба, но универсальна, т.к. не зависит от формы сосуда.

Таким образом, эволюцию БЧ можно представить как последовательность характерных ее этапов:

1) 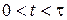- механическая шкала времени, 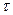– время корреляции случайного взаимодействия 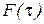. Описание эволюции системы – задача теоретической механики о столкновении многих частиц. Движение полностью детерминировано.

2) 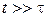– первая грубая шкала времени, детали воздействия среды на частицу смазаны. В качестве динамических ее параметров выступают усредненные по 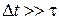величины.

3) При 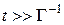устанавливается максвелловское распределение по импульсам, и 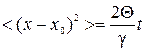. ГУ несущественны.

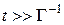– вторая грубая шкала времени. Случайные блуждания БЧ приобретают характер диффузионного процесса. Частица в этом случае не имеет памяти (в механическом смысле) о своей скорости (распределение – максвелловское).

Такие процессы называются марковскими (будущее системы определяется только настоящим и не зависит от ее предыстории). Эволюция системы определяется уравнением Фоккера-Планка. ГУ и НУ существенны.