Неравенства Чебышева

Лекции

По дисциплине курса «Теория вероятностей и математическая статистика»

Часть II

Для студентов специальности

310304 «Информатика»

Минск 2006

ВВЕДЕНИЕ

Математической статистикой называется наука, занимающаяся методами обработки экспериментальных данных (ЭД), полученных в результате наблюдений над случайными явлениями.

Перед любой наукой ставятся следующие задачи:

Ø Описание явлений;

Ø Анализ и прогноз;

Ø Выборка оптимальных решений.

Применительно к математической статистике пример задачи первого типа: пусть имеется статистический материал, представляющий собой случайные числа. Требуется его упростить, представить в виде таблиц и графиков, обеспечивающих наглядность и информативность представленного материала.

Пример задачи второго типа: оценка (хотя бы приблизительная) характеристик случайных величин, например, математического ожидания, дисперсии и т.д. Какова точность полученных оценок.

Одной из характерных задач третьего типа является задача проверки правдоподобия гипотез, которая формулируется следующим образом: можно ли предполагать, что имеющаяся совокупность случайных чисел не противоречит некоторой гипотезе (например о виде распределения, наличия корреляционной зависимости и т.д.).

В курсе рассматриваются задачи всех трех типов: способы описания результатов опыта, способы обработки опытных данных и оценки по ним характеристик случайного явления, способы выбора разумных решений.

ЗАКОН БОЛЬШИХ ЧИСЕЛ

Пусть проводится опыт Е, в котором нас интересует признак Х, или СВ Х. При однократном проведении Е нельзя заранее сказать, какое значение примет Х. Но при n -кратном повторении «среднее» значение величины Х (среднее арифметическое) теряет случайный характер и становится близким к некоторой константе.

Закон больших чисел – совокупность теорем, определяющих условия стремления средних арифметических значений случайных величин к некоторой константе, при увеличении числа опытов до бесконечности (n®¥).

НЕРАВЕНСТВА ЧЕБЫШЕВА

Теорема. Для любой случайной величины X с m_x, D_x выполняется следующее неравенство 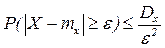где e>0.

Доказательство:

1. Пусть величина Х – ДСВ. Изобразим значения Х и М_х в виде точек на числовой оси Ох

0 х₁ А М_х В

Вычислим вероятность того, что при некотором 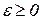величина Х отклонится от своего МО не меньше чем на ε:

.

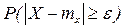Это событие заключается в том, что точка Х не попадет на отрезок [ m_x-ε, m_x+ε ], т.е.

--

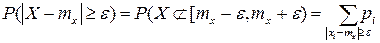для тех значений x, которые лежат вне отрезка [ m_x-ε, m_x+ε ].

Рассмотрим дисперсию с.в. Х:

.

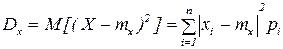Т.к. все слагаемые – положительные числа, то если убрать слагаемые, соответствующую отрезку [ m_x-ε, m_x+ε ], то можно записать:

,

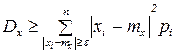т.к. 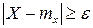, то неравенство можно усилить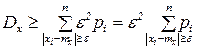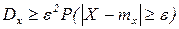

Þ Þ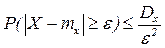

2. Для НСВ:

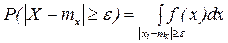
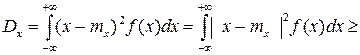
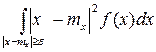- это интегрирование по внешней части отрезка [ m_x-ε, m_x+ε ].

Применяя неравенство 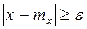и подставляя его под знак интеграла, получаем

.

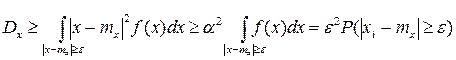Откуда и вытекает неравенство Чебышева для НСВ.

Следствие. 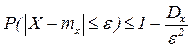- это 2-е неравенство Чебышева.

Доказательство: События 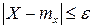и 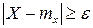- противоположны Þ .

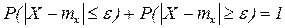1. Лемма: Пусть Х –СВ, e>0 – любое число. Тогда

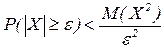
Доказательство:

,

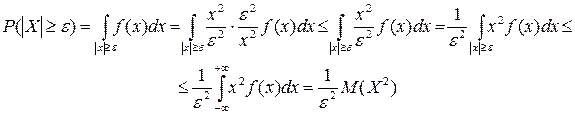Т.к. .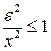

Следствие. .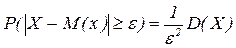

Д-во: Полагаем, вместо св Х – св Х-М(Х), т.к. М(Х-М(Х))²⁼D(X) и получаем неp-во.

Следствие: (правило трех сигм для произвольного распределения):

Полагаем в неравенстве Чебышева 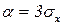, имеем

.

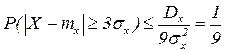Т.е. вероятность того, что отклонение св от ее МО выйдет за пределы трех СКО, не больше 1/9.

Неравенство Чебышева дает только верхнюю границ вероятности данного отклонения. Выше этой границы - значение не может быть ни при никаком распределении.