2015-05-06
322
Ранее было получено выражение МКД точки относительно оси 
:
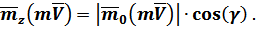
Тогда по аналогии с полученным выражением (18.1.1) будет
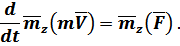
Частный случай, когда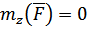 
. Это наблюдается в спиралболе (рис. 22).
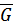– вес; 
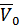– начальная скорость по касательной к окружности.
Моменты сил 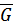и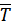 
вокруг оси 
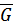равны нолю, так как параллельна оси , а 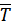пересекает ось.
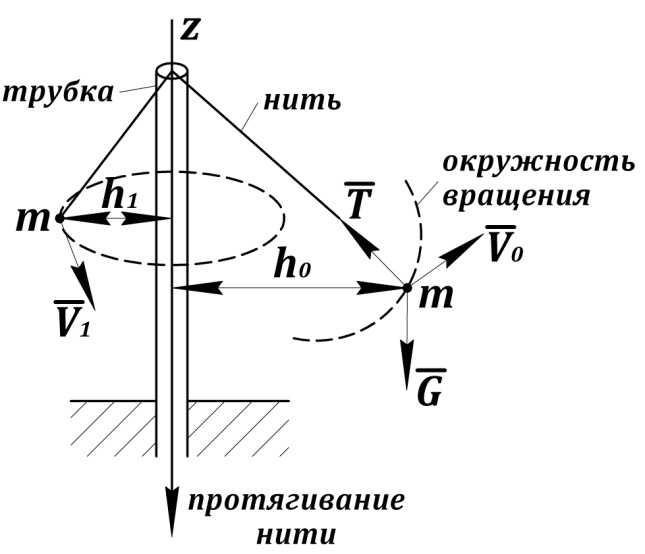
Рис. 22. Изменение момента количества движения точки
относительно оси в спиралболе
При 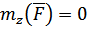будет
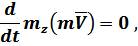
отсюда
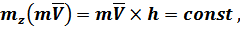
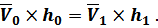
При протягивании нити будет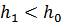 
, тогда
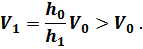
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА МС
