В данной постановке исследования прямолинейных колебаний платформы принимается, что амплитуда возмущающей силы зависит от квадрата частоты колебаний эксцентричной массы:
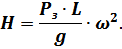
В дифференциальном уравнении вынужденных колебаний платформы, приведённом к единице массы системы, фигурирует амплитуда возмущающей силы, отнесённая к единице массы:
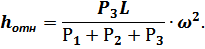
Это выражение для величины 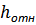 можно записать в следующем виде:
можно записать в следующем виде:
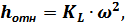
где 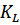 – постоянный коэффициент, м:
– постоянный коэффициент, м:
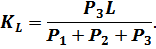
Тогда для амплитуды вынужденных колебаний платформы с учётом вязкого сопротивления получает выражение:
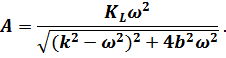
Ниже приведены следующие преобразования, в результате которых получаем:
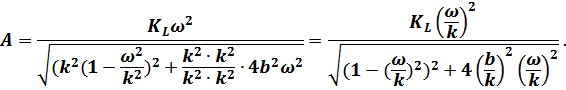
Вводя обозначение для отношения частот 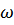 и
и 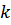
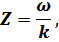
получим для величины 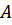 следующее выражение:
следующее выражение:
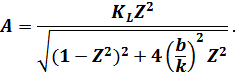
Полученное выражение 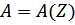 является амплитудной частной характеристикой. Графически эта характеристика отображается резонансными кривыми при различных фиксированных значениях коэффициента
является амплитудной частной характеристикой. Графически эта характеристика отображается резонансными кривыми при различных фиксированных значениях коэффициента 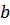 , характеризующего вязкое сопротивление среды.
, характеризующего вязкое сопротивление среды.
В случае
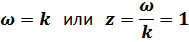 имеет место резонанс. При этом амплитуда
имеет место резонанс. При этом амплитуда 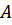 достигает максимума:
достигает максимума:
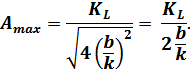
Фазовой частотной характеристикой является зависимость
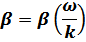
угла отклонения фазы колебаний платформы от фазы колебаний возмущающей силы в установившемся резонансе колебаний, когда величина перемещения платформы определяется выражением:
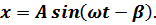
Величина 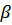 определяется выражением:
определяется выражением:
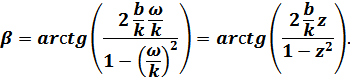
Амплитудная и фазовая частотные характеристики обычно рассматриваются в интервале [0;2] величины  .
.
При вычислении значений величины 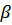 и графическом отображении зависимости
и графическом отображении зависимости
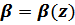
в системе Mathcad необходимо выполнять это раздельно в двух интервалах для  :
: 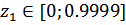 и
и 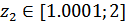 по следующим расчетным формулам:
по следующим расчетным формулам:
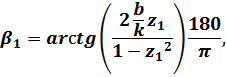
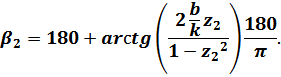
Практическая часть:
С помощью системы MathCAD определим необходимые величины и построим графики колебаний (рис. 32 – 37):

Рис. 32. Исходные данные и начальные вычисления
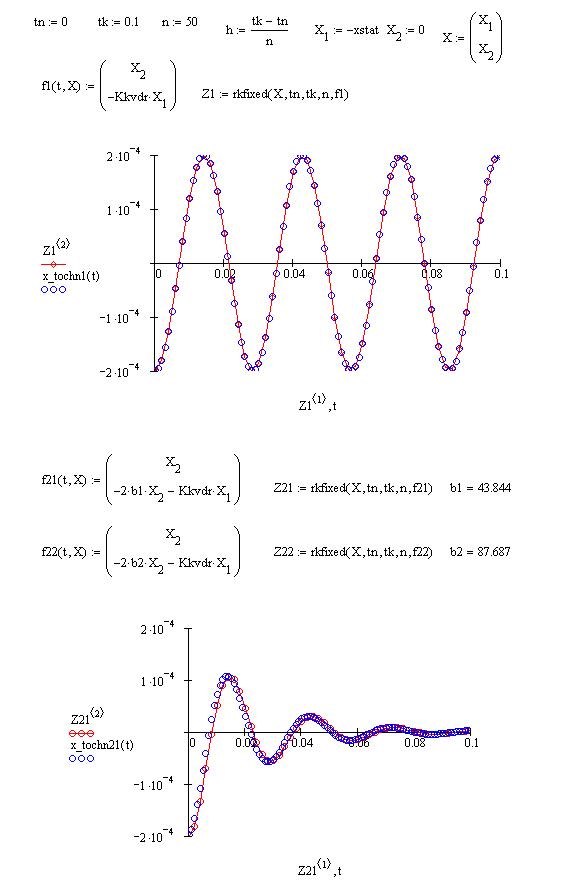
Рис. 33. Законы свободных колебаний без учёта и с учётом сил сопротивления:
сравнение приближённого ( 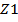 ) и точного (
) и точного ( 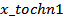 ) решений; сравнение
) решений; сравнение
приближённого ( 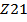 ) и точного (
) и точного ( 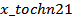 ) решений при коэффициенте вязкости
) решений при коэффициенте вязкости 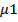
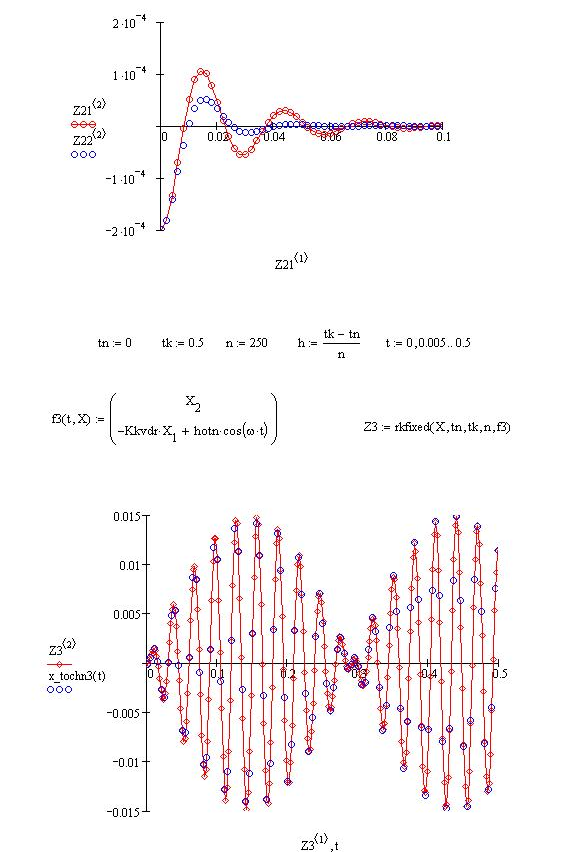
Рис. 34. Закон свободных колебаний с учётом сил сопротивления:
приближённые решения ( 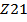 и
и 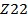 ) при коэффициентах вязкости
) при коэффициентах вязкости 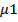 и
и 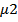 ;
;
закон вынужденных колебаний без учёта сил сопротивления:
сравнение приближённого ( 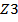 ) и точного (
) и точного ( 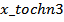 ) решений
) решений
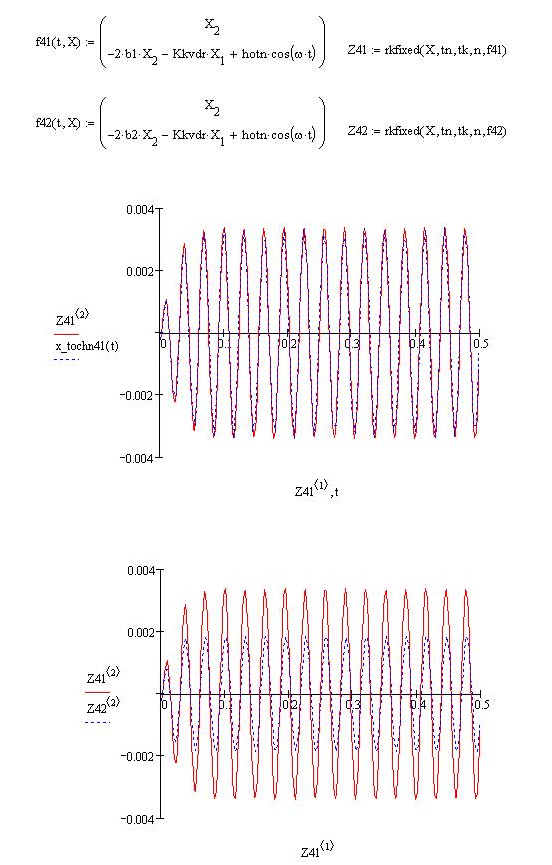
Рис. 35. Законы вынужденных колебаний без учёта и с учётом сил сопротивления:
сравнение приближённого ( 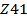 ) и точного (
) и точного ( 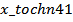 ) решений
) решений
при коэффициенте вязкости 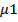 ;
;
приближённые решения ( 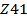 и
и 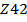 ) при коэффициентах вязкости
) при коэффициентах вязкости 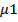 и
и 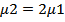
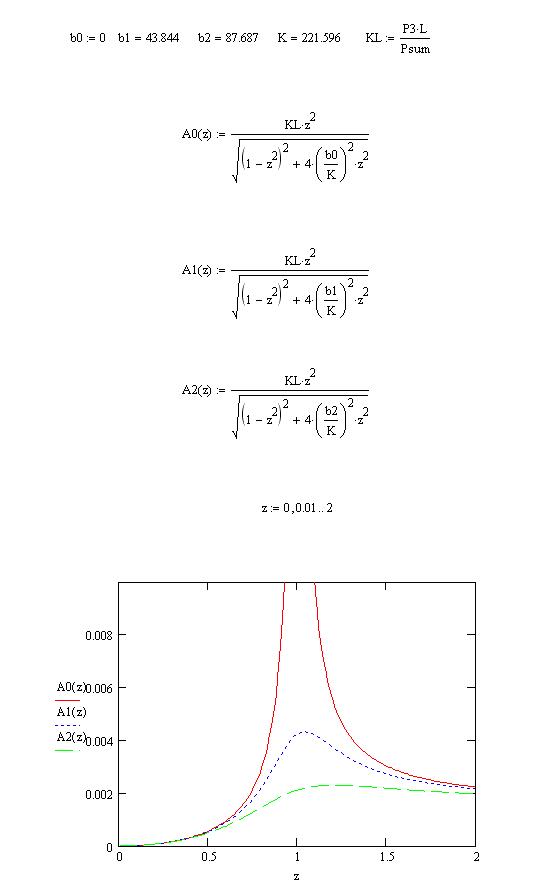
Рис. 36. Амплитудные частотные характеристики в зависимости от отношения частот свободных и вынужденных колебаний 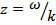 при коэффициентах сопротивления
при коэффициентах сопротивления 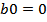 (без учёта сопротивления) и при
(без учёта сопротивления) и при 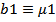 и
и 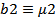
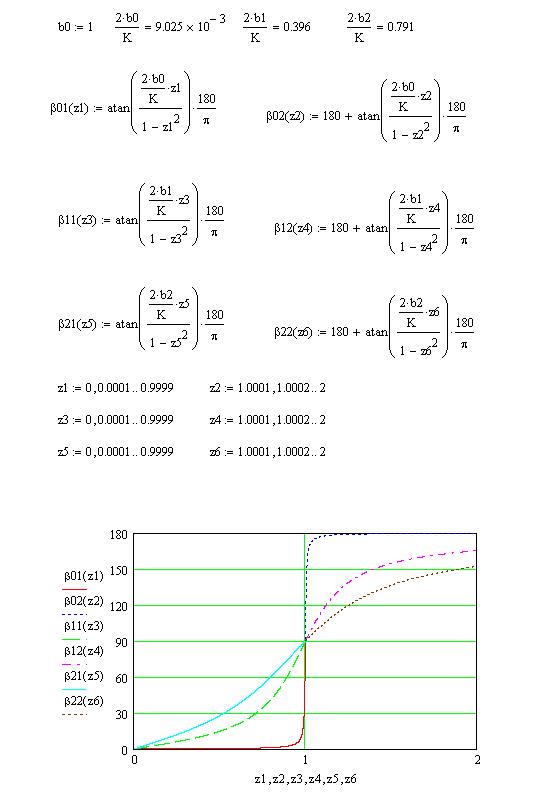
Рис. 37. Фазовые частотные характеристики в зависимости от отношения частот свободных и вынужденных колебаний 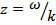 при коэффициентах сопротивления
при коэффициентах сопротивления 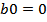 (без учёта сопротивления) и при
(без учёта сопротивления) и при 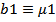 и
и 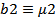
 2015-05-06
2015-05-06 689
689








