Дифференциальное уравнение для данного режима колебаний имеет вид:
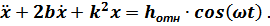
Общее решение этого дифференциального уравнения (при  ) имеет вид:
) имеет вид:
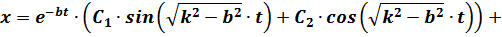
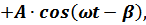
где
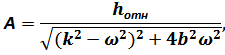
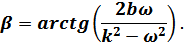
Постоянные интегрирования 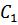 и
и 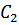 определяются из начальных условий: при
определяются из начальных условий: при 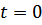 имеем:
имеем:
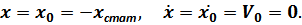
При этих значениях уравнение рассматриваемых колебаний принимает следующий вид:
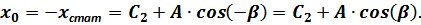
Отсюда:
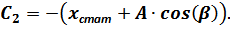
Далее имеем:
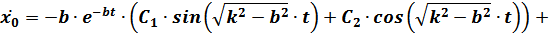
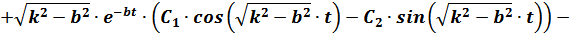
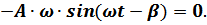
Отсюда при 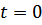 :
:
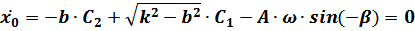
или
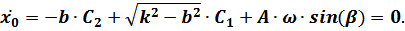
После подстановки в это уравнение выражения 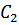 получим:
получим:
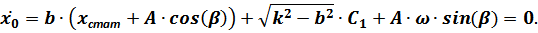
Отсюда:
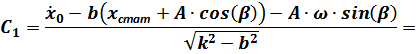
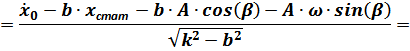
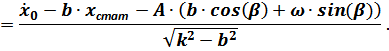
После подстановки выражений 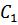 и
и 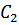 в выражение
в выражение 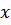 получим:
получим:
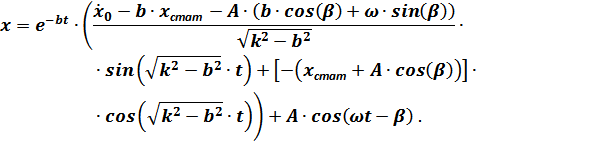
После перегруппировки членов выражения для 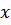 с целью анализа слагаемых процесса колебаний платформы оно примет вид:
с целью анализа слагаемых процесса колебаний платформы оно примет вид:
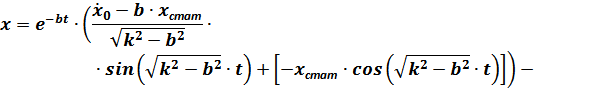
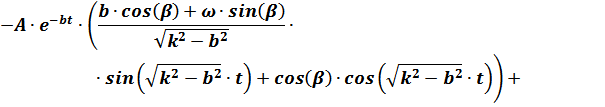
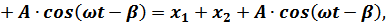
где 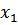 – характеризует свободные (собственные) затухающие колебания платформы, зависящие от начальных данных
– характеризует свободные (собственные) затухающие колебания платформы, зависящие от начальных данных 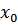 и
и 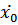 (в данном примере
(в данном примере  ), а также зависящие от параметров системы
), а также зависящие от параметров системы 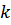 и
и 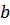 :
:
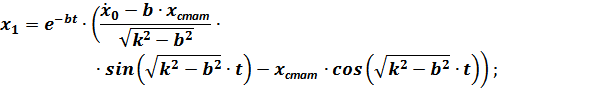
х2 – характеризует добавочные затухающие колебания платформы, обусловленные действием возмущающей силы и протекающие при определённом сочетании параметров системы со значительно большими начальными амплитудами, а следовательно, дольше затухающие, чем собственные затухающие колебания, зависящие от начальных данных 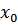 и
и 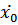 :
:
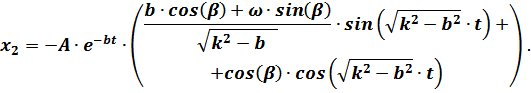
Для численного решения дифференциального уравнения второго порядка вынужденного колебаний платформы с учётом сил сопротивления это уравнение заменяется системой из двух уравнений первого порядка по аналогии с режимом свободных колебаний с учётом сил сопротивления:
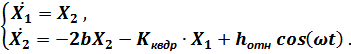
 2015-05-06
2015-05-06 2426
2426
