При направлении оси 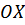 вверх имеем следующее выражение дифференциального уравнения этих колебаний:
вверх имеем следующее выражение дифференциального уравнения этих колебаний:
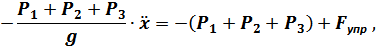
где 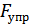 – упругая восстанавливающая сила опор платформы при дополнительном смещении платформы вниз на величину
– упругая восстанавливающая сила опор платформы при дополнительном смещении платформы вниз на величину 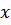 .
.
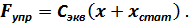
После подстановки величины 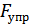 в дифференциальное уравнение получим:
в дифференциальное уравнение получим:
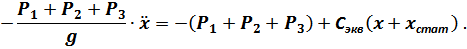
С учётом условия начального равновесия:
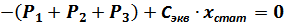
получим следующее выражение дифференциального уравнения:
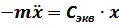
или
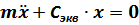 ,
,
где 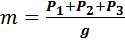 .
.
Дифференциальное уравнение свободных колебаний платформы можно записать в следующем виде:

где 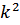 – квадрат круговой частоты свободных колебаний, 1/с2:
– квадрат круговой частоты свободных колебаний, 1/с2:
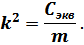
Из теории дифференциальных уравнений общее решение этого уравнения имеет вид:
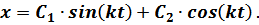
Из начальных условий имеем при 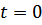 :
:
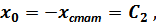
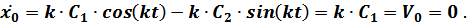
Отсюда:
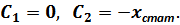
В итоге получаем уравнение – закон свободных колебаний платформы без учёта сил сопротивления:
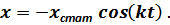
Для численного решения дифференциального уравнения второго порядка свободныеколебания без учёта сил сопротивления удобно преобразовать его к системе из двух уравнений первого порядка. Для этого обозначим:

Тогда получим следующую систему:
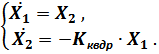
Начальные условия для интегрирования этой системы:

6.2 Свободные колебания с учётом сопротивления.
В этом режиме сила сопротивления среды, пропорциональна скорости движения платформы:
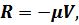
где 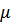 – коэффициент вязкости среды, Н/(м/с).
– коэффициент вязкости среды, Н/(м/с).
С учётом фактора сопротивления дифференциальное уравнение свободных колебаний платформы записывается в следующем виде:
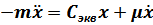
или
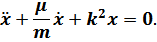
Обычно данное дифференциальное уравнение приводят к виду:
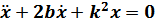 ,
,
где 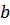 – коэффициент сопротивления среды,
– коэффициент сопротивления среды,  .
.
Из сравнения двух видов дифференциальных уравнений получаем:
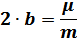
или
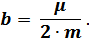
Единица измерения величины 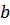 :
:
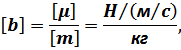
Так как Н = кг ∙ м / с2, то получаем:
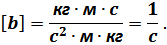
Из теории дифференциальных уравнений общее решение полученного дифференциального уравнения имеет вид:
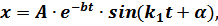
где 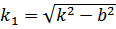 ,
,
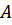 и
и 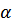 – начальные амплитуда и фаза колебаний, определяемые из начальных условий.
– начальные амплитуда и фаза колебаний, определяемые из начальных условий.
Это дифференциальное уравнение получено из общего решения, записанного в виде:
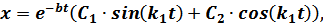
где постоянные интегрирования 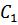 и
и 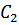 представляются в виде:
представляются в виде:
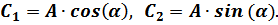
Тогда:
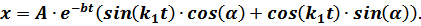
Отсюда по известной формуле тригонометрии для синуса суммы двух углов 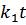 и
и 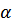 получается первоначально приведённое общее решение дифференциального уравнения. Из начальных условий имеем при
получается первоначально приведённое общее решение дифференциального уравнения. Из начальных условий имеем при 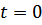 :
:
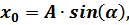
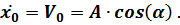
Из равенства
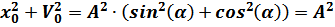
получаем:
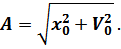
Из выражений
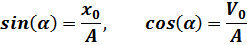
получаем:
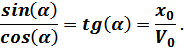
При начальных условиях колебаний платформы, а именно:

имеем:
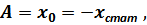
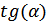 стремится к бесконечности, значит
стремится к бесконечности, значит
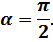
При найденных величинах 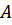 и
и 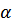 решение дифференциального уравнения свободных колебаний платформы с учётом сил сопротивления имеет вид:
решение дифференциального уравнения свободных колебаний платформы с учётом сил сопротивления имеет вид:
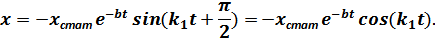
Для численного решения дифференциального уравнения второго порядка свободных колебаний платформы с учётом сил сопротивления это уравнение заменяется системой из двух уравнений первого порядка по аналогии с режимом свободных колебаний без учёта сил сопротивления:
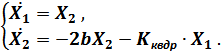
Для сравнения процессов затухания при расчёте используются два значения коэффициента затухания 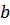 :
:
1) 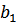 при
при 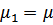 из исходных данных,
из исходных данных,
2) 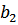 при
при 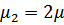 .
.
 2015-05-06
2015-05-06 779
779








