В данной постановке исследования прямолинейных колебаний платформы принимается: амплитуда возмущающей силы зависит от квадрата частоты колебаний эксцентричной массы:
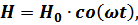
где 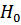 – амплитуда возмущающей силы, Н:
– амплитуда возмущающей силы, Н:
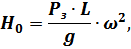
где 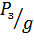 – значение эксцентричной массы, кг,
– значение эксцентричной массы, кг,
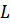 – расстояние от оси электродвигателя до центра тяжести эксцентричной массы, м.
– расстояние от оси электродвигателя до центра тяжести эксцентричной массы, м.
Дифференциальное уравнение для данного режима колебаний имеет вид:
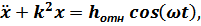
где 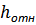 – амплитуда возмущающей силы, отнесённая к единице массы системы, м/с2:
– амплитуда возмущающей силы, отнесённая к единице массы системы, м/с2:
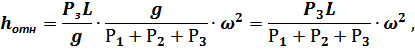
где
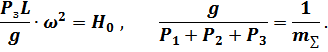
Общее решение дифференциального уравнения для данного режима колебаний складывается из решений для свободных и вынужденных колебаний:
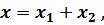
где
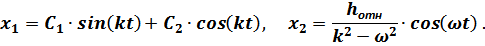
Тогда:
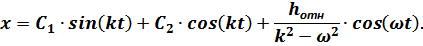
Постоянные интегрирования 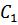 и
и 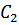 определяются из начальных условий. При
определяются из начальных условий. При 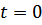 имеем:
имеем:

При этих значениях уравнение рассматриваемых колебаний принимает следующий вид:
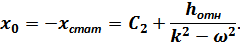
Отсюда:
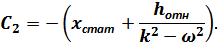
Далее имеем:
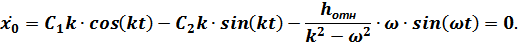
Отсюда при 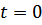 получается
получается 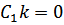 , т.е.
, т.е. 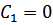 .
.
Закон колебаний в данном режиме:
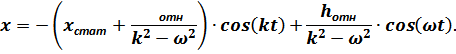
Для численного решения дифференциального уравнения второго порядка вынужденных колебаний платформы без учёта сил сопротивления это уравнение заменяется системой из двух уравнений первого порядка по аналогии с режимом свободных колебаний без учёта сил сопротивления:
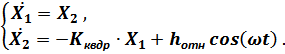
 2015-05-06
2015-05-06 1678
1678
