Спектральное представление можно обобщить на случай, когда функция x(t) непериодическая, T®¥. На основании (2.4.2) и (2.4.3), учитывая 1/T=w1/2p, имеем
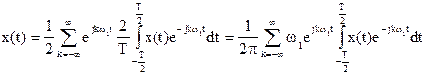 .
.
При T®¥ сумма переходит в интеграл, величина 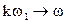 , а
, а 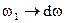 , где w - текущая непрерывная частота. Тогда получим:
, где w - текущая непрерывная частота. Тогда получим:
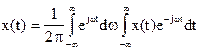
или 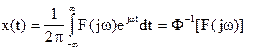 , (2.4.6)
, (2.4.6)
где 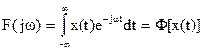 . (2.4.7)
. (2.4.7)
Формулы (2.4.7) и (2.4.6) определяют соответственно прямое и обратное преобразование Фурье. В них Ф и Ф-1 - обозначение прямого и обратного операторов Фурье.
Формулы (2.4.7) и (2.4.6) - пара интегральных преобразований Фурье. Функция F(jw) называется спектральной функцией или комплексным спектром непериодического сигнала. Она определена при положительных и отрицательных частотах.
Значения спектральной функции при положительных и отрицательных значениях частоты w комплексно сопряжены. Поэтому (2.4.6) можно записать в виде
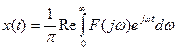 ,
,
где Re - обозначение взятия действительной части.
Интеграл Фурье (2.4.7) представляет непериодическую функцию в виде суммы бесконечного числа бесконечно малых по амплитуде и бесконечно близких по частоте гармонических колебаний 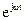 . Поэтому непериодическая функция имеет непрерывный, т. е. сплошной, спектр. Другими словами, в непериодической функции имеются все частоты.
. Поэтому непериодическая функция имеет непрерывный, т. е. сплошной, спектр. Другими словами, в непериодической функции имеются все частоты.
Согласно (2.4.6), комплексная амплитуда элементарного колебания 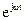 равна
равна
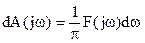 .
.
Отсюда следует
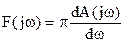 ,
,
т. е. спектральная функция характеризует не амплитуду, а спектральную плотность амплитуд.
Спектральную функцию можно представить в виде
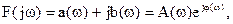
где 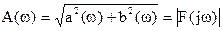 - спектр амплитуд (тоже характеризует не амплитуду, а спектральную плотность амплитуд);
- спектр амплитуд (тоже характеризует не амплитуду, а спектральную плотность амплитуд);
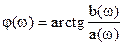 - спектр фаз.
- спектр фаз.
2.4.3. Связь преобразований Фурье
Сравнение (2.4.1) и (2.4.2) дает:
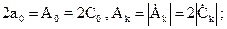
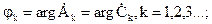
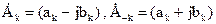 .
.
Сравнение (2.4.2) и (2.4.7) позволяет записать:
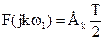 и
и 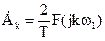 .
.
Сравнение (2.4.4) и (2.4.7) дает:
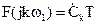 и
и 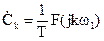 .
.
Отсюда следует, что для сигналов одинаковой формы дискретная функция 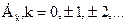 вписывается в непрерывную функцию
вписывается в непрерывную функцию
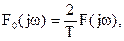
которую называют огибающей дискретного спектра периодического сигнала. 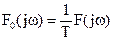 .
.
 2015-05-06
2015-05-06 574
574








