Аналитическое или графическое представление сигналов как функции частоты является представлением сигналов в спектральной (частотной) области.
Различают представление сигналов в спектральной области с дискретным и сплошным спектрами.
Можно доказать, что периодические сигналы обладают дискретными спектрами, а одиночные и пачечные сигналы – сплошными.
Пусть некоторый периодический сигнал представлен совокупностью u(t) гармонических колебаний: 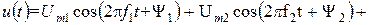
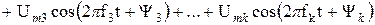 .
.
Совокупность частот 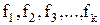 представленных колебания является частотным спектром данного сигнала.
представленных колебания является частотным спектром данного сигнала.
Совокупность амплитуд на соответствующих частотах
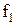
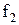
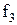 …
… 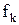
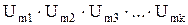
является амплитудно-частотным спектром данного сигнала.
Совокупность начальных фаз на соответствующих частотах
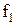
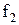
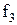 …
… 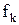
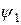
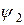
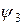 ...
... 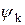
является фазо-частотным спектром данного сигнала.
Амплитудно-частотный спектр (АЧС) (рис. 1.19) и фазо-частотный спектр (ФЧС) (рис. 1.20) могут быть изображены в виде системы, состоящей из двух графиков.
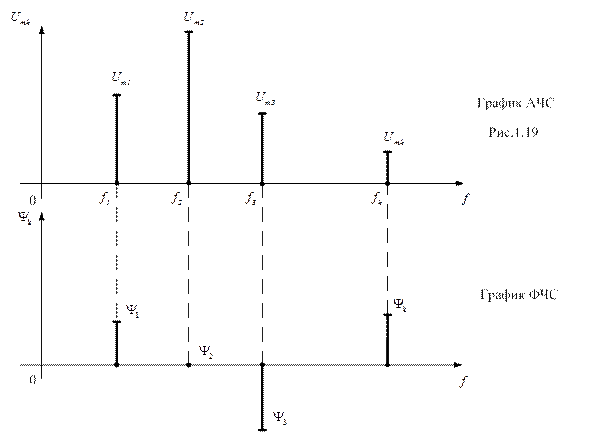
Рис. 1.20
Для одиночных и пачечных сигналов АЧС и ФЧС будут сплошными.
Для расчета спектров, т.е. для представления сигналов как функции частоты, используют следующие основные приемы:
· тригонометрические преобразования,
· интегральное преобразование Фурье,
· разложение в ряд Фурье.
В результате интегрального преобразования Фурье вычисляют спектральную плотность заданного одиночного сигнала и представляют ее в показательной форме записи
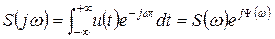 ,
,
здесь 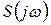 – спектральная плотность,
– спектральная плотность, 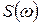 – модуль спектральной плотности,
– модуль спектральной плотности, 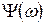 – аргумент спектральной плотности,
– аргумент спектральной плотности, 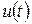 – сигнал.
– сигнал.
Аналитические выражения 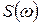 или
или 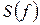 , а так же
, а так же 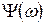 или
или 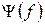 являются зависимости, описывающими АЧС и ФЧС данного сигнала.
являются зависимости, описывающими АЧС и ФЧС данного сигнала.
В результате разложения в ряд Фурье представляют заданный периодический сигнал в виде совокупности гармонических составляющих:
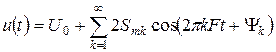 ,
,
где 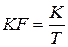 – частота гармонической составляющей с номером
– частота гармонической составляющей с номером 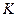 ,
, 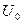 - постоянная составляющая,
- постоянная составляющая, 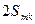 – амплитуда гармонической составляющей с номером K,
– амплитуда гармонической составляющей с номером K, 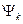 – начальная фаза гармонической составляющей с номером
– начальная фаза гармонической составляющей с номером 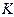 .
.
Расчет 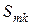 и
и 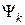 проводится согласно выражению
проводится согласно выражению
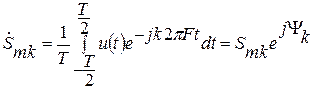 ,
,
где 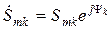 - комплексная амплитуда ряда Фурье.
- комплексная амплитуда ряда Фурье.
Расчет 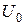 проводится аналогично, при
проводится аналогично, при 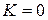 :
:
Между спектральной плотностью 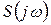 и комплексной амплитудой ряда Фурье существует связь:
и комплексной амплитудой ряда Фурье существует связь:
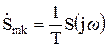 ,
, 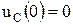 ,
,
которая позволяет, зная значения спектральной плотности, вычислить комплексную амплитуду ряда Фурье путем вычисления спектральной плотности на частотах 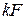 и умножения полученных значений на множитель
и умножения полученных значений на множитель 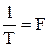 .
.
 2015-05-06
2015-05-06 1091
1091
