Спектральный метод анализа

В основе спектрального метода анализа лежит использование свойств частотного коэффициента передачи системы и спектрального представления сигналов.

Основная формула. Пусть на входе некоторой стационарной системы действует детерминированный сигнал U _вх(t), заданный своим разложением в интеграл Фурье:

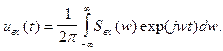(6.18)

Будем полагать, что математическая модель системы задана частотным коэффициентом передачи K(jw). Как уже известно, комплексный сигнал exp(jwt) является собственной функцией рассматриваемой системы, создавая на выходе элементарную реакцию K(jw)exp(jwt). Поэтому спектральное представление выходной реакции можно записать в виде:

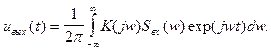(6.19)

Полученная таким образом основная формула спектрального метода свидетельствует о том, что частотный коэффициент передачи служит множителем пропорциональности между спектральными плотностями сигналов на входе и на выходе:

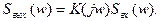(6.20)

Итак, анализ систем в частотной области обладает замечательным свойством: эффект преобразования сигнала в системе отображается просто алгебраической операцией умножения. Следует иметь в виду, что спектральный и временной подходы полностью эквивалентны друг другу. Действительно, интеграл Дюамеля есть свертка функций U _вх(t) и импульсной характеристики во временной области: U_вых(t) = U _вх(t)*h(t), а значит, спектральная плотность выходного сигнала есть произведение спектров функций U _вх(t) и h(t). Отсюда непосредственно следует формула (6.20).

Коэффициент передачи многокаскадных систем. Для радиотехники характерно использование сложных систем, отдельные звенья которых включены каскадно, т.е. выходной сигнал предыдущего звена служит входным сигналом для последующего. Примером такой системы может служить многокаскадный усилитель.

Будем полагать, что известны частотные коэффициенты передачи отдельных звеньев K_n(jw), n = 1, 2,..., N, где N – общее число каскадов. Подавая на вход первого каскада сигнал и_вх (t)=exp(jwt), получаем на выходе

и_вых (t) = K₁(jw) K₂(jw)...K_N(jw) exp(jwt),

откуда результирующий коэффициент передачи системы

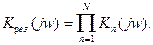(6.21)

В практике инженерных расчетов широко применяется способ выражения АЧХ систем в логарифмических единицах – децибелах. Если на некоторой частоте w известен модуль частотного коэффициента передачи, то усиление системы на этой частоте, выраженное в децибелах, равно

D = 20 lg /K(jw)/. (6.22)

Система, для которой K(jw) < 1, ослабляет сигнал; этому случаю соответствует отрицательное усиление.

Легко видеть, что при каскадном соединении звеньев их усиления алгебраически суммируются:

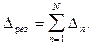(6.23)

Частотный коэффициент передачи мощности. Используя формулу Рэлея и равенство Парсеваля, энергию выходного сигнала можно определить по формуле:

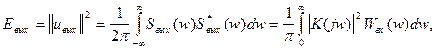(6.24)

где W_вх(w) – энергетический спектр сигнала на входе.

Тогда в соответствии с (6.24) W_вых(w) = ïK(jw)ï² W_вх(w). Величину

K_p(w) = ïK(jw)ï² (6.25)

называют частотным коэффициентом передачи мощности системы на заданной частоте w. Вещественность этого коэффициента делает вычисление энергии выходного сигнала гораздо более простой задачей по сравнению с поиском точной формы выходного сигнала, тем более, что во многих случаях вполне достаточно знать лишь изменение энергии сигнала, прошедшего линейную систему.

Автокорреляционная характеристика системы. Автокорреляционная характеристика системы Q(t) определяется как преобразование Фурье от частотного коэффициента передачи мощности:

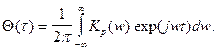(6.26)

Помимо частотного представления возможно и временное представление функции (6.26). Учитывая, что K_p(w) = K(jw) K*(jw), можно предположить, что между функциями K_p(w) и Q(t) должна существовать такая же связь, как и между энергетическим спектром и функцией автокорреляции произвольного сигнала:

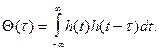(6.27)