Спектр дельта-функции

Дельта-функцией называется сигнал вида (рис. 1.23):

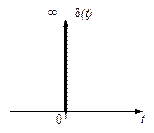
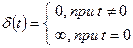
Рис. 1.23

Спектральную плотность получим путем вычисления интеграла

.

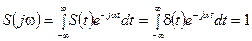Такой результат является следствием так называемого фильтрующего свойства дельта-функции(1.24), которое заключается в следующем

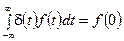, т. к. 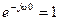, то ,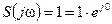

поэтому , .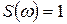

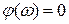График спектра показанный на рисунке 1.25. Амплитудно-частотный спектр на всех частотах одинаков и равен 1. Фазо-частотный спектр на всех частотах равен 0. АЧС является сплошным и ширина спектра бесконечна.

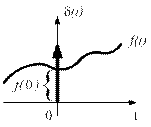
Рис.1.24

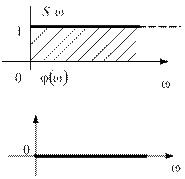
Рис.1.25

Начальные фазы всех гармонических колебаний (рис. 1.26) одинаковы и равны 0. Это значит, что в момент времени 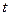= 0 все составляющие, изменяющиеся по косинусоидальному закону, проходят через амплитудное значение. В этот момент их сумма образует бесконечную величину.

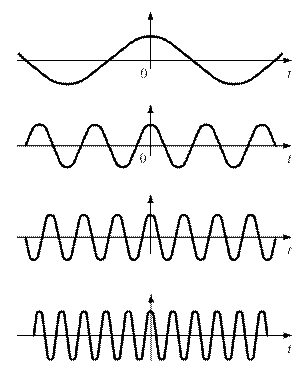
Рис.1.26