Определения некоторых понятий и терминов

Вариации коэффициент - безразмерная мера рассеяния случайной величины относительно математического ожидания:

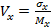, (В-1)

где σ - стандартное отклонение случайной величины, M_x - математическое ожидание. Коэффициент вариации был предложен в 1895 году К. Пирсоном. Выборочный коэффициент вариации вычисляется по формуле:

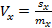, (В-2)

где s_x - квадратичное отклонение случайной величины, m_x - оценка математического ожидания. В практике экспериментальных исследований коэффициент вариации служит также оценкой точности (воспроизводимости) эксперимента; в этих случаях его называют относительной ошибкой и выражают в процентах.

Воспроизводимость в теории и практике экспериментальных исследований - характеристика точности лабораторного или промышленного эксперимента, а также подтверждение результатов тех или иных наблюдений в природе и обществе другими исследователями в другое время в тех или иных условиях. Проблема воспроизводимости связана с тем, что абсолютное совпадение результатов экспериментов проводимых в одинаковых условиях невозможно. Рассеяние результатов экспериментов возникает по двум причинам: неточное измерение физических характеристик (ошибки измерений) и неизбежные изменения условий экспериментов при повторении опытов, даже если опыты проводятся при усиленном контроле.

Обычно воспроизводимость характеризуется количественно - коэффициентом вариации (В-2), (т.е. числом, в процентах или долях единицы), но может характеризовать явление или процесс и качественно. Движения звёзд, планет, комет и т.д. воспроизводятся с высокой точностью. Воспроизводимость некоторых событий в природе явилась причиной возникновения так называемых народных примет. См. также Дисперсия воспроизводимости.

Выборка - понятие математической статистики, объединяющее результаты каких-либо однородных наблюдений. Выборкой в широком смысле слова называется массив результатов наблюдений X₁, X₂,..., X_n, представляющих собой независимые, одинаково распределённые случайные величины. Определённая таким образом выборка называется случайной, а её конкретные значения в каждом отдельном случае x₁, x₂,..., x_n - простой выборкой. С точки зрения исследователя, осуществляющего экспериментальные исследования с целью моделирования процесса, выборкой будет называться конкретное количество анализов, опытов, измерений и т.п., а под совокупностью будет подразумеваться абстрактная бесконечность возможных анализов, опытов, измерений и т.п.

Для различения параметров совокупности и параметров выборки последние принято обозначать латинскими буквами, например, выборочная дисперсия s²_x, квадратичное (стандартное) отклонение s_x, в отличие от генеральной дисперсии σ²_x и генерального стандарта σ_x. Аналогично, математическое ожидание M_x, а его оценка m_x.

Генеральная дисперсия - дисперсия совокупности σ²_x. См. также Выборка, Дисперсия, Совокупность.

Генеральный стандарт - стандартное (квадратичное) отклонение совокупности σ_x. См. также Выборка, Квадратичное отклонение, Совокупность, Стандартное отклонение.

Дисперсия в математической статистике и теории вероятностей - центральный момент второго порядка, одна из характеристик распределения вероятностей случайной величины, наиболее употребительная мера рассеяния её значений относительно центра, т.е. отклонения её от среднего значения.

В теории вероятностей дисперсия, DX, случайной величины X определяется как математическое ожидание E(X-M_x)² квадрата отклонения X от её математического ожидания M_x=EX. Для случайной величины X с непрерывным распределением, имеющим плотность вероятности p(x), дисперсия определяется формулой:

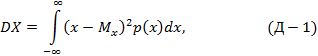
если этот интеграл сходится. Если DX=0, то случайная величина X принимает с вероятностью 1 единственное значение M_x. Дисперсия имеет важное значение в характеристике качества статистической оценки случайной величины. Наряду с дисперсией в качестве меры рассеяния (той же размерности, что и сама случайная величина) используется квадратный корень из дисперсии: σ= 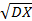, называемый квадратичным отклонением X.

Поскольку в реальной жизни математическое ожидание - величина неизвестная, на практике определяют среднее значение выборки и выборочную дисперсию:

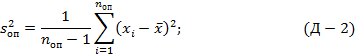
где

где n_оп - число опытов в выборке, ν_оп=n_оп-1 - число степеней свободы выборочной дисперсии.

Для оценки результатов наблюдений одной дисперсии недостаточно. Корень квадратный из выборочной дисперсии называется квадратичным отклонением, стандартным отклонением или стандартом.

С точки зрения ценности информации о поведении случайной величины то, чем больше дисперсия (т.е. больше разброс значений случайной величины относительно центра распределения), тем оценка M_x хуже, информация о сущности явления, процесса разнесена на большем интервале. При сближении значений стандартного отклонения и среднего значения информативность уменьшается, а если в результате обработки данных получено x_ср<s_x, то либо ошибки измерений велики, либо в явлении, процессе отсутствует физическая сущность. См. также Выборка, Дисперсия воспроизводимости.

Дисперсия воспроизводимости - количественная характеристика точности эксперимента или воспроизводимости результатов наблюдений в природе, науке, технике и технологии; вычисляется по формуле:

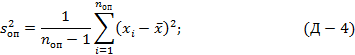
где x - среднее значение:

где n_оп - число опытов на воспроизводимость; ν_оп=n_оп-1 - число степеней свободы дисперсии воспроизводимости.

С точки зрения метода моментов дисперсия воспроизводимости является центральным моментом второго порядка и для непрерывной случайной величины может быть вычислена по формуле:

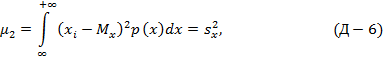
Для оценки достоверности результатов наблюдений одной дисперсии воспроизводимости недостаточно. Корень квадратный из дисперсии воспроизводимости называется квадратичным отклонением, стандартным отклонением или стандартом. Начинающие исследователи обычно с трудом развивают интуитивное восприятие численного значения дисперсии или стандартного отклонения. Является ли дисперсия воспроизводимости, равная, например, 77, большой или малой? Что значит стандартное отклонение 0,51∙10^-4? Оказывается, для интерпретации как дисперсии воспроизводимости, так и стандартного отклонения главное не получить численные значения последних, а правильно сравнить дисперсию воспроизводимости с какой-либо другой дисперсией, например, дисперсией адекватности или стандартное отклонение с соответствующим параметром, чтобы проверить нулевую гипотезу (гипотезу об отсутствии различия). На начальных этапах исследований стандартное отклонение ±s_x сравнивают со средним значением выборки, x_ср. Если |s_x|«x_ср, то говорят о значимом отличии результатов наблюдений от нуля и предварительную оценку точности эксперимента осуществляют по отношению s_x/x_ср (по коэффициенту вариации). Если коэффициент вариации лежит в пределах 3÷4%, то в первом приближении результаты наблюдений считают воспроизводимыми; в противном случае необходимы дополнительные изыскания. См. также Дисперсия.

Доверительная вероятность - вероятность достоверности принимаемой гипотезы, характеристика надёжности, полученной по выборке оценки того или иного параметра:

P=P{|M_x-m_x|≤ε_p}, (Д-7)

где M_x - генеральный параметр (в данном случае математическое ожидание); m_x - его оценка; ε_p =f(p) - ошибка определения генерального параметра; P - вероятность настолько большая, что событие |M_x-m_x|≤ε_p можно считать практически достоверным. Очевидно, что диапазон возможных с вероятностью P значений ошибки от замены M_x на m_x равен ± ε_p. Вероятность появления ошибок, больших по абсолютной величине, чем ε_p, или вероятность событий |M_x-m_x|≥ε_p называется уровнем значимости:

α=1-P=P{|M_x-m_x|≥ε_p }. (Д-8)

Иначе доверительная вероятность может быть интерпретирована как вероятность того, что неизвестное значение измеряемой величины M_x находится в пределах:

m_x- εp≤Mx≤m_x+ ε_p, (Д-9)

где выборочный параметр m_x, по существу, случайная величина, а ошибка его определения (M_x-m_x) также случайная величина. Интервал I_p=m_x± ε_p называется доверительным интервалом. Границы интервала m_x,min=m_x- ε_p и m_x,max=m_x+ ε_p называются доверительными границами. Доверительный интервал при принятой доверительной вероятности определяет точность оценки. Величина доверительного интервала зависит от принимаемой доверительной вероятности, т.е. от той вероятности, с которой гарантируется нахождение искомого параметра M_x внутри доверительного интервала. Другими словами: чем выше гарантия надёжности оценки, тем больше величина интервала, в котором может находится генеральный параметр. В исследованиях прикладного характера доверительная вероятность обычно принимается P=0,95. Соответственно, уровень значимости α=1-P=0,05. В случае нормально распределённой случайной величины это соответствует вероятности попадания случайной величины в интервал M_x-2σ≤X≤M_x+2σ или, по аналогии с вероятностью 0,997, правилу двух сигма (вероятность попадания случайной величины в интервал P(M_x-3σ≤X≤M_x+3σ)=0,997 называется правилом трёх сигма).

Доверительное отклонение - функция от результатов наблюдений и доверительной вероятности, позволяющая оценить доверительный интервал, который с вероятностью P=1-α "накрывает" неизвестное значение параметра:

где s_x - квадратичное (стандартное) отклонение; n - количество наблюдений в выборке; t - критерий Стьюдента, зависящий от числа степеней свободы ν выборочной дисперсии и уровня значимости α. Необходимо отметить, что доверительное отклонение не зависит ни от математического ожидания M_x, ни от генерального параметра σ_x. Это случайная величина, зависящая только от квадратичного отклонения s_x и принимаемого исследователем уровня значимости α. См. также Доверительные границы.

Доверительные границы - интервал значений, с доверительной вероятностью P=1-α "накрывающего" неизвестное значение параметра M_x исследуемого явления или процесса:

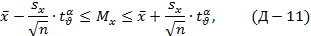
ф где 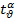- случайная величина, зависящая только от числа степеней свободы ν выборочной дисперсии и уровня значимости α, s_x - стандартное отклонение. Этим соотношением пользуются практически при обработке экспериментальных данных для определения доверительного интервала x_ср. Эта задача была решена в 1908 г. У.С.Госсетом (William Sealy Gosset; 1876-1937), известным под псевдонимом Student. Очевидно, что выражение:

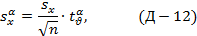
характеризует доверительное отклонение среднего значения выборки. Необходимо отметить, что уровнем значимости исследователь задаётся независимым путём, т.е. исходя из сущности задачи, природы процесса, явления. См. также Доверительное отклонение.

Квадратичное отклонение, квадратичное уклонение, величин x₁, x₂,..., x_n от α - выражение:

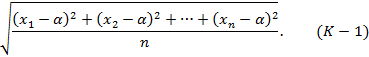
Наименьшее значение квадратичное отклонение имеет при α=x_ср, где x_ср - среднее арифметическое величин x₁, x₂,..., x_n:

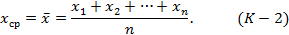
Употребляется также более общее понятие взвешенного квадратичного отклонения, определяемого как выражение:

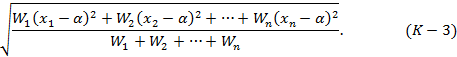
числа W₁, W₂,..., W_n называют при этом весами, соответствующими величинам x₁, x₂,..., x_n. Взвешенное квадратичное отклонение достигает наименьшего значения при α, равном взвешенному среднему. Такое представление о квадратичном отклонении соответствует использованию квадратичного отклонения в теории ошибок.

В теории вероятностей и математической статистике квадратичное отклонение σ_x случайной величины X (от её математического ожидания) определяют как квадратный корень из дисперсии 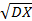и в англо-американской литературе называют стандартным отклонением величины X или просто стандартом. В отечественной литературе квадратичное отклонение σ_x случайной величины X называют генеральным стандартом, а дисперсию совокупности σ²_x - генеральной дисперсией.

В практических задачах, приводящих к нормальному распределению, отклонения больше, чем утроенный стандарт (квадратичное отклонение) практически невозможны, или, другими словами, на практике пренебрегают возможностью отклонений от среднего, больших 3σ_x (правило трёх сигма).

Математическое ожидание - мера центральной тенденции в рассеянии случайной величины, одна из важнейших характеристик распределения вероятностей случайной величины. Понятие математического ожидания случайной величины используется для теоретических построений при исследовании распределений вероятностей случайных величин и для решения различных задач.

В некоторых азартных играх математическое ожидание можно указать абсолютно точно (например, математическое ожидание результата бросания двух игральных костей - семь). Отличительной особенностью азартных игр является однозначно трактуемый результат: успех-неудача, целое число очков, характеристика карты и т.д.

Для непрерывной случайной величины математическое ожидание выражается формулой:

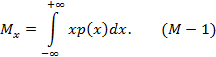
Выражение (М-1) является математическим выражением координаты центра тяжести, т.е. M_x можно представить себе как абсциссу центра тяжести массы, расположенной под кривой, являющейся плотностью вероятности p(x). Это выражение аналогично формуле для начального момента первого порядка:

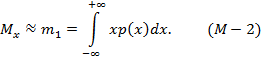
Для физических величин, определяемых в результате наблюдений и экспериментов, математическое ожидание определить невозможно, его можно только оценить.

Примечание: в формуле (М-2) знак "≈" поставлен потому, что в результате эксперимента получают выборку из совокупности, и в этом случае начальный момент первого порядка будет являться одной из возможных оценок математического ожидания.

В научных и прикладных исследованиях математическое ожидание характеризует наиболее вероятное значение физической величины, получаемой в результате экспериментального определения, но оно отличается от моды, которая характеризует расположение максимума кривой p(x). Проблема любого наблюдения и эксперимента заключается в том, что значение какой-либо характеристики явления или процесса абсолютно точно определить невозможно. В результате многократных измерений физической величины получится множество значений, имеющих большее или меньшее рассеяние относительно среднего значения. По существу, все результаты экспериментов являются случайными величинами, имеющими то или иное распределение вероятностей. Принято считать, что это среднее значение является оценкой неизвестного математического ожидания (истинного значения измеряемой величины).

В большинстве случаев математическое ожидание характеризует наиболее вероятное расположение значений случайной величины. Название "математическое ожидание" происходит от понятия "ожидаемого значения выигрыша" (математического ожидания выигрыша), впервые появившегося в теории азартных игр в трудах Б.Паскаля, П.Ферма и Х.Гюйгенса в XVII в. Они ввели понятие математического ожидания случайного события и использовали его для решения ряда задач, в том числе весьма старинной задачи (ставшей с тех пор классической) о разделе ставки в неоконченной игре. Понятие "математическое ожидание" в 1795 г. ввёл П.Лаплас. В полной мере это понятие было оценено и использовано в сер. XIX в. русским математиком П.Л.Чебышевым (1821-1894).

Исходы азартных игр по вполне понятным причинам выражаются целыми числами или двумя возможными взаимоисключающими исходами ("успехом" и "неудачей"), поэтому в ряде случаев математическое ожидание можно определить точно (например, подбрасывание монеты, бросание двух, трёх и более игральных костей, причём математическое ожидание в этих случаях является ещё и модой, и медианой). Результаты наблюдений и экспериментов (за редким исключением) - числа действительные (вещественные), включающие в себя, помимо истинной физической компоненты, также ошибки случайные, систематические и грубые. По этим причинам в наблюдениях и экспериментальных исследованиях математическое ожидание - понятие достаточно абстрактное, и степень этой абстрактности связана как с асимметрией распределения физической случайной величины, так и с асимметрией распределения ошибок измерений.

Существует несколько способов оценки математического ожидания по результатам выборки, но только некоторые из них используются практически. В большинстве случаев важно знать среднее значение выборки или совокупности, которое удовлетворяло бы некоторому критерию, соответствующему физической сущности задачи. Наибольшее значение имеют четыре вида среднего значения, - мода, медиана, среднее арифметическое и начальный момент первого порядка.

Максимуму кривой плотности вероятностей соответствует мода, это наиболее вероятный результат. Мода в статистике - то, что в обычной жизни называется массовым, типичным. Например, цена, по которой данный товар чаще всего реализуется на рынке.

Если распределение асимметрично, то иногда представляет интерес медиана, x_0,5 - то значение случайной величины, которое делит распределение на две равные части. Другими словами, вероятности событий по обе стороны медианы одинаковы. Мода и медиана имеют больше теоретическое, чем практическое значение - для экспериментальной выборки моду и медиану вычислить непросто. Следующим средним значением является среднее арифметическое, его проще всех вычислить, и отчасти по этой причине оно нашло наиболее широкое применение. Кроме этого, в условиях нормально распределённых ошибок наблюдений арифметическое среднее имеет наименьшую дисперсию, точнее, арифметическое среднее является состоятельной, несмещённой и эффективной

оценкой математического ожидания. В условиях асимметричных кривых распределения медиана расположена между модой и средним арифметическим.

Следует заметить, что кроме арифметического среднего в науке и технике применяют также: арифметическое взвешенное среднее, x_ср,w, взвешенное степенное среднее, x_w,α, гармоническое среднее, x_h, геометрическое среднее, x_g, квадратичное среднее, x_s, кубическое среднее, x_cub, арифметико-геометрическое среднее, x_ср,g и начальный момент первого порядка, m₁; при этом x_h<x_g<x_ср<x_s<x_cub (см. Среднее, среднее значение).

Медиана, в теории вероятностей и математической статистике, - одна из числовых характеристик распределения вероятностей случайной величины. Для непрерывно распределённой случайной величины X строго монотонной функции распределения F(x) медиана m определяется как единственный корень уравнения F(x)=1/2 (или как квантиль K_1/2), т.е. условием, что случайная величина X принимает с вероятностью 1/2 как значения, большие x_0,5, так и значения, меньшие x_0,5. В общем случае медиана определяется неоднозначно, но для любой случайной величины существует, по крайней мере, одна медиана; в симметричном случае медиана (если она единственна) совпадает с математическим ожиданием, если оно существует. В условиях асимметричных кривых распределения медиана расположена между средним значением и модой.

Мода - одна из числовых характеристик распределения вероятностей случайной величины. Для случайной величины, имеющей плотность вероятности p(x), модой называется любая точка максимума p(x). Распределения с одной, двумя или большим числом максимумов называется соответственно унимодальными (или одновершинными), бимодальными или мультимодальными. Для многовершинных распределений понятие моды теряет смысл. Мода в статистике - то, что в обычной жизни считается массовым, типичным. Примером моды является цена, по которой данный товар чаще всего реализуется на рынке. В отличие от среднего арифметического вероятная ошибка определения моды поддаётся оценке в редких случаях.

Момент - (мат.) Одна из числовых характеристик распределения вероятностей случайной величины. Начальным моментом порядка β (β>0, целое) непрерывной случайной величины X называется выражение:

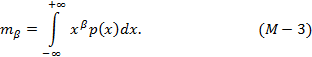
Начальный момент первого порядка или первый начальный момент характеризует математическое ожидание случайной величины. Математическое ожидание определяет положение центра, вокруг которого группируются все возможные значения случайной величины. Оценка математического ожидания для непрерывной случайной величины определяется формулой:

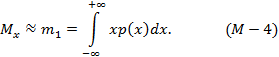
Примечание: в формуле (М-4) знак "≈" поставлен потому, что в результате эксперимента получают выборку из совокупности, и в этом случае начальный момент первого порядка будет являться одной из возможных оценок математического ожидания.

Центральным моментом β-того порядка для непрерывной случайной величины называется выражение:

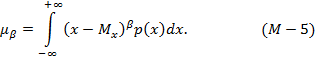
Второй центральный момент характеризует рассеивание случайной величины относительно математического ожидания и называется дисперсией, обозначаемой s²_x. Для непрерывной случайной величины определяется формулой:

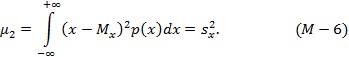
Имеется прямая аналогия моментов в математическое статистике с моментами, играющими важную роль в механике: момент первого порядка (оценка математического ожидания M_x) аналогичен статическому моменту, центральный момент второго порядка μ₂ (дисперсия s²) - моменту инерции, соответствующей формулой определяется момент распределения масс.

Наблюдение - метод исследования предметов и явлений реальности в том виде, в каком они существуют и происходят в природе и обществе. Наблюдение отличается от простого восприятия информации наличием цели и активной позицией наблюдателя. Наблюдение отличается и от эксперимента отсутствием активного управляющего воздействия на явление или процесс. Наблюдение - это фиксация характерных признаков предмета или развития явления в пространстве и/или во времени.

Несмещённая оценка - статистическая оценка параметра распределения вероятностей, вычисленная по результатам наблюдений, лишённая систематической ошибки. Например, если результаты наблюдений x₁, x₂,..., x_n являются взаимно независимыми случайными величинами, имеющими одинаковое нормальное распределение, то среднее арифметическое:

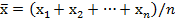(Н-1)

будет несмещённой оценкой для M_x. Используемая ранее для оценки σ²_x выборочная дисперсия:

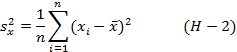
не является несмещённой оценкой, так как среднее арифметическое само зависит от элементов выборки. Для устранения смещения оценки нужно число степеней свободы в выражении для s²_x уменьшить на единицу. Несмещённой оценкой для σ²_x служит:

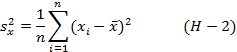
Оценка - количественная характеристика параметра, получаемая по результатам выборки. Проблема оценки неизвестного параметра является одной из центральных в теории обработки результатов наблюдений. К оценкам параметров предъявляется комплекс требований. Важнейшие среди них: несмещённость, состоятельность и эффективность. Важно отметить, что в отличие от математического ожидания (некоторой неизвестной абстрактной величины, меры центральной тенденции распределения случайной величины) оценок математического ожидания множество, например, арифметическое взвешенное среднее, арифметико-геометрическое среднее, арифметическое среднее, взвешенное степенное среднее, гармоническое среднее, геометрическое среднее, среднее квадратичное, среднее кубическое, а также мода, медиана и начальный момент первого порядка:

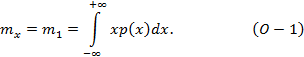
Очевидно, что разные виды средних различаются; отсюда возникает проблема правильного выбора формы среднего значения. Решающую роль здесь играет физическая сущность объекта (процесса, явления), а также интуиция и добросовестность исследователя.

Случайная величина - величина, значение которой невозможно предсказать исходя из условий эксперимента или наблюдений. Почти все результаты измерений физических величин по существу случайные величины. Случайные величины могут изменяться непрерывно (температура, давление, концентрация, радиус частиц дисперсной фазы) или дискретно (число "очков" в азартной игре, число частиц, число дефектов, число отказов, аварийность). По мнению В. Феллера, понятие "случайная величина" в некоторой степени некорректно, более подходящим был бы термин "функция случая". Дело в том, что независимой переменной является положение точки в пространстве элементарных событий, т.е. результаты эксперимента, наблюдения или реализация того или иного случая.

Событие - то, что произошло, то или иное уникальное явление, случившийся факт. Событие становится достоверным, если в данном конкретном сочетании факторов оно необходимо осуществляется. Событие рассматривается случайным, если оно может осуществиться, а может и не осуществиться. Изолированных событий в природе нет, все события осуществляются или не осуществляются в той или иной определённой системе событий. Событие может быть причиной, может быть следствием. Событие как явление окружающего нас мира может пройти незамеченным, а может быть целью. В последнем случае можно говорить о событии как результате наблюдения.

Совокупность - 1. Сообщество, сочетание, соединение, общее число, сумма. 2. мат. Понятие теории статистического выборочного метода. В математической статистике совокупностью называется множество каких-либо однородных элементов, из которого по определённому правилу выделяется некоторое подмножество, называемое выборкой. Например, при приёмочном статистическом контроле в роли совокупности выступает множество всех изделий, подлежащее общей характеризации. В простейших случаях контролируемая выборка извлекается из совокупности случайно (наугад), что с точки зрения теории вероятностей означает: если совокупность содержит N элементов и отбирается выборка из n элементов (n<N), то выбор должен быть осуществлён таким образом, чтобы для любой группы из n элементов вероятность быть извлечённой равнялась n!(N-n)!/N!.

В практике экспериментальных исследований и в математической статистике выборкой из совокупности принято также называть результаты измерений какой-либо физической величины, подверженной случайным ошибкам. В этом случае под совокупностью подразумеваются все возможные значения физической величины. Для решения практических задач бесконечное множество значений интереса не представляет; практический интерес представляют те или иные характеристики соответствующей функции распределения F(x). В этом случае выборка из бесконечной совокупности представляет собой наблюдаемые значения нескольких случайных величин, по которым определяются необходимые параметры.

Следует различать параметры совокупности и параметры выборки. Параметры совокупности принято обозначать греческими буквами, например математическое ожидание M_x, генеральная дисперсия σ²_x, генеральный стандарт σ_x. Параметры выборки принято обозначать соответствующими латинскими буквами, например, выборочная дисперсия s²_x, квадратичное (стандартное) отклонение s_x. Поскольку оценок математического ожидания много, в общем случае, среднее значение обозначают m_x.

Состоятельность оценки - статистическая оценка параметра распределения вероятностей, обладающая тем свойством, что при увеличении числа наблюдений вероятность отклонений оценки от оцениваемого параметра на величину, превосходящую некоторое наперёд заданное малое число, стремится к нулю. Другими словами, оценка m_x, вычисленная по выборке размерности n, будет состоятельной оценкой для M_x, если для любых сколь угодно малых положительных чисел ε и η, существует N такое, что вероятность неравенства:

|m_x – M_x| < ε, (С-1)

больше 1-η для всех n>N.

Попроще - оценка параметра называется состоятельной, если по мере роста числа наблюдений n→ 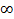она стремится к математическому ожиданию оцениваемого параметра. Так, выборочное среднее и выборочная дисперсия представляют собой состоятельные оценки соответственно математического ожидания и дисперсии нормального распределения.

Среднее, среднее значение совокупности чисел x₁, x₂,..., x_n - концептуальное число, заключённое между наименьшим и наибольшим из них и получаемое из элементов совокупности при помощи некоторой процедуры, которая как раз и определяет специфический вид среднего значения. Среднее значение может быть целью исследования, а может привлекаться для характеристики совокупности в целом как один из моментов или как оценка математического ожидания. Среднее значение совокупности выражает равнодействующую влияния множества факторов на вариацию признака независимо от вида распределения случайной величины. Среднее значение подобно центру тяжести - точке, через которую проходит равнодействующая сил тяжести всех элементов выборки. Таким образом, можно говорить об уравновешивании отклонений от среднего значения в асимметричном распределении, а непосредственное взаимопогашение отклонений от среднего значения, присущее нормальному распределению, рассматривать как частный случай уравновешивания (проявление закона равновесия), которое не изменяет природы среднего значения и отклонений от него.

Среднее значение - понятие математической статистики, по существу, некоторая абстрактная величина, зависящая от метода вычисления (т.е. от концепции) и в случае арифметического среднего удовлетворяющая условию метода наименьших квадратов:

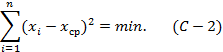
Иногда условие (С-2) записывают в более простом, но нереальном виде:

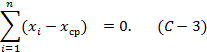
В научных исследованиях технологических процессов в большинстве случаев особых проблем с исчислением среднего значения не возникает. Наиболее употребительным средним является арифметическое среднее:

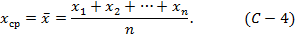
Если результаты наблюдений x₁, x₂,..., x_n являются взаимно независимыми случайными величинами, имеющими одинаковое нормальное распределение, то среднее арифметическое будет несмещённой, состоятельной и эффективной оценкой математического ожидания M_x. Вероятная ошибка определения среднего арифметического всегда поддаётся оценке.

Если переменные величины x_i имеют различные частоты или вес, правильнее вычислять арифметическое взвешенное среднее:

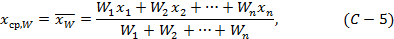
где W_i - частота или вес i-того наблюдения. Среди всех линейных оценок взвешенное среднее арифметическое обладает минимальной дисперсией.

Примером приложения арифметического взвешенного среднего в технологии строительства скважин является средний взвешенный диаметр бурильной колонны:

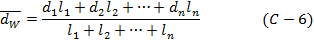
где d_i - диаметр i-того элемента бурильной колонны, l_i - длина i-того элемента, n - количество элементов в бурильной колонне. Необходимо добавить, что применительно к среднему диаметру бурильной колонны понятие математического ожидания теряет смысл.

В науке, технике и технологии кроме арифметического среднего ш1.0

применяют также взвешенное степенное среднее:

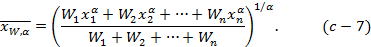
Если частоты или веса всех наблюдений равны, то формула (С-7) упрощается:

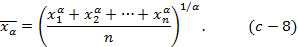
Степень α определяет конкретный вид среднего значения. При α=-1 общая формула степенного среднего превращается в гармоническое среднее, т.е. в среднее из обратных величин:

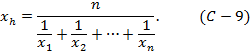
При α=0 получим геометрическое среднее:

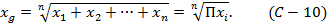
Примером среднего геометрического является средний диаметр частиц твёрдой фазы неправильной формы:

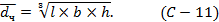
где l, b, h - максимальные длина, ширина, высота частицы.

При α=1 получим формулу среднего арифметического (С-4).

При α=2 получим формулу среднего квадратичного:

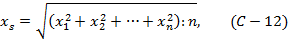
При α=3 получим формулу среднего кубического:

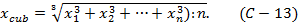
В науке, технике и технологии находит применение также арифметико-геометрическое среднее, x_ср,g. Арифметико-геометрическое среднее - общий предел последовательностей арифметического среднего x_ср,n и геометрического среднего x_g,n, получаемых в результате следующих операций. Для пары положительных чисел a и b вычисляют арифметическое среднее x_ср,1 и геометрическое среднее x_g,1. Далее для пары x_ср,1 и x_g,1 снова вычисляют арифметическое среднее x_ср,2 и геометрическое среднее x_g,2 и т.д. В результате получают последовательность чисел x_ср,n и x_g,n, n=1, 2,... Вычисления продолжают до получения результата с требуемой точностью.

Анализ формулы (С-7) позволяет определить соотношения между различными видами среднего. Чем больше значение α, тем больше величина среднего значения; при этом получается следующая цепочка неравенств:

x_h<x_g<x_ср,g< 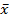<x_s<x_cub. (С-14)

Например, если x₁=1, x₂=2, x₃=3, то x_h=1,636; x_g=1,817; x_ср,g=1,9075; x_ср=2; x_s=2,161; x_cub=2,29. Дисперсии, соответственно равны: s²_h=1,1987; s²_g=1,0502; s²_ср,g=1,0128; s²_ср=1,0; s²_s=1,0389; s²_cub=1,1262. См. таблицу 1.

Очевидно, что разные виды средних различаются; отсюда возникает проблема правильного выбора формы среднего значения. Также очевидно, что у арифметического среднего минимальная дисперсия. Другими словами, арифметическое среднее является эффективной статистической оценкой. Если ошибки измерений подвержены закону нормального распределения, то состоятельной, несмещённой и эффективной оценкой неизвестного математического ожидания будет арифметическое среднее, а все остальные оценки смещены относительно M_x.

Таблица 1.

Вид среднего значения	Среднее значение	Дисперсия
Гармоническое Геометрическое Арифметико- геометрическое Арифметическое Квадратичное Кубическое	1,636 1,817 1,9075 2,0 2,161 2,29	s2h=1,1987; s2g=1,0502; s2ср,g=1,0128; s2ср=1,0; s2s=1,0389; s2cub=1,1262.

Решающую роль в решении проблемы выбора формы среднего значения играет физическая сущность объекта (процесса, явления), интуиция и добросовестность исследователя.

Следует отметить, что задача поиска среднего значения для симметрично распределённой случайной величины решается относительно просто. В этом случае можно говорить о взаимной компенсации противоположных влияний множества факторов, влияющих на результат наблюдения (эксперимента). Иное дело - несимметричное распределение. В асимметричном распределении случайной величины противоположные влияния различных факторов не компенсируют друг друга, и результаты наблюдений концентрируются либо слева, либо справа от середины диапазона распределения, кроме этого распределение может быть островершинным и плосковершинным, и, иногда, иметь два максимума.

Для таких распределений среднее значение выражает равнодействующую влияния всех факторов на вариацию случайной величины. Среднее значение подобно центру тяжести - точке, через которую проходит равнодействующая всех гравитационных сил. В IV в. до Р.Х. по

нятия среднего значения не было, интуитивная и неформализованная идея об оптимальных свойствах средних исходила от Аристотеля ('Aristotelhz; 384-322 до Р.Х.) - понятие "истинная середина", учение о достоинствах среднего поведения, средней уверенности, средней умеренности и т.д. "Прекрасна во всём середина: мне по душе ни избыток, ни недостаток" (Демокрит (Dhmokritoz); 460/470 - 360/370 г. до Р.Х.).

В III в. до Р.Х. Архимед ('Arcimhdhz; ок. 287-212 до Р.Х.) ввёл понятие "центр тяжести", соответствующее понятию среднего значения. В учебнике Теона Смирнского (II в.) идёт речь о разработке центрального члена непрерывной пропорции (в то время ещё не различали понятия среднего значения и пропорции). Разработку определения центрального члена непрерывной пропорции следует, по-видимому, считать началом развития понятия среднего значения. А в XX в. статистик У.Дж.Рейхман написал: "Каждый понимает, что такое средние, до тех пор, пока не начнёт применять их".

Стандартное отклонение - то же, что квадратичное отклонение. Корень квадратный из выборочной дисперсии.

Стандартные границы - интервал значений величины, с неизвестной вероятностью p "накрывающего" неизвестное значение параметра M_x исследуемого явления или процесса:

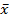- s_x ≤ M_x ≤ 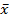+ s_x, (С-15)

где s_x - стандартное отклонение. Этим соотношением пользуются практически при обработке экспериментальных данных, при определении коэффициента вариации V_x и решении вопроса о точности экспериментов или наблюдений. Среднее значение выборки определяют по формуле:

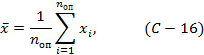
а выборочную дисперсию по формуле:

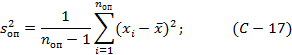
где n_оп - число опытов в выборке, ν_оп=n_оп-1 - число степеней свободы выборочной дисперсии.

Стандартное отклонение (квадратичное отклонение или стандарт) определяют по формуле:

Для оценки результатов наблюдений одной дисперсии недостаточно. Корень квадратный из выборочной дисперсии называется квадратичным отклонением, стандартным отклонением или стандартом.

Степеней свободы число - (мат.) число независимых источников информации при вычислении какого-либо параметра, характеризующего совокупность. Число степеней свободы характеризует информационный потенциал выборки, это всегда целое положительное число:

ν=n-l. (С-19)

где n - размерность выборки, l - число параметров, вычисленных по данным выборки. Например, при вычислении дисперсии воспроизводимости вместо математического ожидания M_x используют среднее значение выборки, вычисляемое по данным выборки. При этом происходит потеря одной степени свободы, поскольку дисперсия вычисляется при этом по n_оп-1 независимым источникам информации. Таким образом ν_оп=n_оп-1.

Число параметров, определённых по выборке, ещё называется числом связей, наложенных на выборку. Так вот, с точки зрения теории информатики число степеней свободы равно числу параметров, которое ещё можно определить по выборке после той или иной обработки, а с точки зрения математической статистики ν равно числу независимых источников информации, по которым вычисляется тот или иной выборочный параметр. Дело в том, что, используя одну и ту же выборку, невозможно решить сразу две задачи: оценить параметры совокупности и применить соответствующий критерий для проверки достоверности полученных оценок без какой-либо компенсации, связанной с двукратным обращением к имеющемуся массиву наблюдений. Такой компенсацией является уменьшение знаменателя в формуле выборочной дисперсии от числа наблюдений n до числа независимых источников информации оцениваемого параметра ν. Если, например, математическое ожидание M_x оценивается по результатам пяти независимых наблюдений:

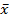= (x₁+x₂+x₃+x₄+x₅)/5; (С-20)

то результат имеет пять степеней свободы. Дисперсия оценивается по пяти квадратам разностей (x_i-x_ср)², однако независимо вычисляются только четыре из этих разностей, так как, определив четыре, пятую уже можно вычислить следующим образом:

x⁵- 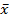= 4 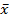-(x₁+x₂+x₃+x₄). (С-21)

Поэтому имеется только четыре независимых источника информации, по которым вычисляется выборочная дисперсия. Бывают случаи, когда в качестве оценки математического ожидания M_x используется величина, не зависимая от рассматриваемой выборки (например m_x), т.е. оценка определяется независимым путём. В таких случаях для выборочной дисперсии следует пользоваться формулой:

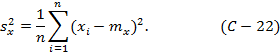
Стьюдента критерий, t-критерий - критерий значимости, основанный на распределении Стьюдента и используемый для проверки гипотез о средних значениях нормально распределённых физических величин и для проверки на значимость оценок параметров. Случайная величина t, характеризующая соотношение неизвестной ошибки определения M_x и стандартного отклонения s_x:

имеет распределение Стьюдента или t-распределение; плотность вероятностей p(t) этой случайной величины имеет вид колоколообразной кривой. В соотношении (С-23) ν=n-1 - число степеней свободы.

Пусть результаты наблюдений x₁, x₂,..., x_n - взаимно не зависимые, нормально распределённые случайные величины с неизвестными параметрами M_x и σ². При отсутствии грубых и систематических ошибок результат первоначальной обработки наблюдений x_ср совпадает с математическим ожиданием M_x с большей или меньшей точностью, зависящей от объёма выборки n:

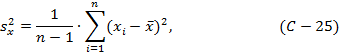
где 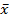- оценка математического ожидания M_x, в частности, арифметическое среднее, а s²_x - оценка генеральной дисперсии σ². В тех случаях, когда s_x≈|x_ср| или s_x≥|x_ср|, говорят, что "оценка x_ср математического ожидания M_x незначимо отличается от нуля"; в этом случае может быть два исхода: либо M_x=0, либо M_x 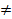0, в обоих случаях необходимо повысить точность проведения наблюдений (эксперимента) и/или увеличить объём выборки. В тех случаях, когда s_x«|x_ср| и возникает задача собственно оценки точности наблюдений, а более строго, определения интервала значений, с той или иной вероятностью "накрывающего" неизвестное значение параметра исследуемого распределения. Эта задача была решена в 1908 г. У.С.Госсетом (William Sealy Gosset; 1876-1937), известным под псевдонимом Student:

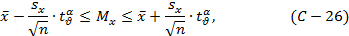
где 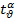- случайная величина, зависящая только от числа степеней свободы ν выборочной дисперсии и уровня значимости α. Соотношение (С-26) характеризуют интервал значений, с доверительной вероятностью P=1-α "накрывающего" неизвестное значение параметра исследуемого распределения, этим соотношением пользуются практически при обработке экспериментальных данных для определения доверительного интервала x_ср. Очевидно, что выражение:

характеризует доверительное отклонение среднего значения выборки. Необходимо отметить, что уровнем значимости исследователь задаётся независимым путём, т.е. исходя из сущности задачи, природы процесса, явления.

Необходимо различать односторонний и двусторонний критерии Стьюдента. Если по физической сущности задачи опытный критерий Стьюдента может располагаться по обе стороны нуля, то следует брать двусторонний критерий, если по одну - односторонний. Значение двустороннего критерия Стьюдента берётся из таблицы для вдвое меньшего принимаемого исследователем уровня значимости.

Табличные значения критерия Стьюдента для различных уровней значимости α приведены в Приложении 2.

Уровень значимости статистического критерия - вероятность ошибочно отвергнуть основную (нулевую) проверяемую гипотезу, когда она верна. Понятие "уровень значимости" возникло в связи с задачей проверки согласованности теории с опытными данными. Если, например, в результате наблюдений регистрируются значения n случайных величин X₁, X₂,..., X_n и требуется по этим данным проверить гипотезу H₀, согласно которой совместное распределение величин X₁, X₂,..., X_n обладает некоторым определённым свойством, то соответствующий статистический критерий конструируется с помощью подходящим образом подобранной функции θ=f(X₁, X₂,..., X_n). Эта функция обычно принимает малые значения, когда гипотеза H₀ верна, и большие значения, когда H₀ ложна; такую гипотезу ещё называют гипотезой об отсутствии различия, или нулевой гипотезой. Соответствующий критерий значимости представляет собой правило, согласно которому значимыми считаются значения θ, превосходящие некоторое критическое значение θ^α. В свою очередь выбор величины θ^α определяется заданным уровнем значимости α, который в случае отклонения гипотезы H₀ совпадает с вероятностью события {θ> θ^α}. Центральный момент при проверке гипотезы H₀ заключается в том, что уровнем значимости α задаются до анализа выборки на основании физической сущности задачи и последствий от ошибочного принятия решения. Диапазон значений уровней значимости, принимаемых в науке и технике, достаточно широк: 0,001; 0,01; 0,02; 0,05; 0,1; 0,2 и т.д. Наиболее употребительно значение a=0,05; оно соответствует доверительной вероятности P=0,95 или, по аналогии с вероятностью 0,997 (правило трёх сигма), правилу двух сигма, т.е. вероятности попадания нормально распределённой случайной величины в интервал (M_x-2σ≤X≤M_x+2σ). Соответствующая вероятность P=0,954. При этом следует иметь в виду, что общая вероятность (общая площадь под кривой плотности вероятностей гипотетического критерия p(θ)) равна единице, а уровень значимости α соответствует площади под крайней ветвью кривой при θ> θ^α.

В теории статистической проверки гипотез уровень значимости называется вероятностью ошибки первого рода. Вероятность такой ошибки не больше принятого уровня значимости. Например, при α=0,05 можно совершить ошибку первого рода в пяти случаях из ста. Принятие основной проверяемой гипотезы, когда она неверна, называется ошибкой второго рода. Фиксация уровня значимости находится целиком в компетенции исследователя: он должен решать, какой риск при отклонении нулевой гипотезы является допустимым.

Подробнее см. Дэвис­Дж.С. "Статистический анализ данных в геологии": Пер. с англ. В 2 кн./Пер. В.А.Голубевой, под ред. Д.А.Родионова.- М.:Недра, 1990.- 427­с.: ил., а также "Разнообразие форм уравнений парной регрессии": Учебное пособие/ Д.Н.Цивинский; Самар. гос. техн. ун-т. Самара, 2002, 80 с.

Эксперимент - (1) научно поставленный лабораторный или промышленный опыт, наблюдение исследуемого процесса в фиксируемых условиях; возможность многократного воспроизводства процесса в требуемых или повторяющихся условиях; (2) опыт вообще, попытка осуществить чего-либо. Нередко главной задачей эксперимента является проверка гипотез и предсказаний теории, имеющих принципиальное значение. В этом случае эксперимент выполняет функцию критерия истинности научного познания в целом.

Эффективность оценки - свойство оценки иметь больший или меньший доверительный интервал. Оценка параметра называется эффективной, если среди нескольких оценок того же параметра она обладает наименьшей дисперсией. Если ошибки измерений физических величин подчинены закону нормального распределения, то среднее арифметическое обладает наименьшей дисперсией.

Таблица П.2.