Структуры порождающей и проверочной матриц ЛБК определяются характеристиками формируемого кода. Порождающая матрица ЛБК имеет размерность n×k и состоит из двух подматриц: информационной и проверочной. Число столбцов информационной подматрицы равно k, а число столбцов проверочной подматрицы равно r. Число строк обеих подматриц одинаково и равно.
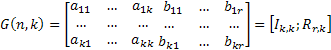 [1]
[1]
В качестве информационной подматрицы при канонической форме выбирают единичную матрицу.
 [2]
[2]
Проверочная подматрица по Варшамову строится путем подбора различных т-разрядных, комбинаций, удовлетворяющих следующим условиям:
1. Количество единиц в строке (вес строки) должно быть не менее dmin-1.
2. Сумма по модулю 2 двух любых строк должна иметь не менее dmin-2 единиц.
Единичная матрица в канонической форме может находится либо перед матрицей проверочных элементов, либо после нее, в зависимости от того, где в кодовой комбинации располагаются информационные элементы (в начале или в конце комбинации).
Аналитическое описание ЛБК с использованием проверочных матриц:
Если записать правило формирования каждого из проверочных соотношений кодовой комбинации в виде вектора из 0 и 1, где 1указывают, какие элементы кодовой комбинации охвачены проверкой на четность, то получим n-k векторов. Так как каждый проверочный вектор отражает проверку на четность, введенную для любой кодовой комбинации, то справедливо следующее свойство линейных ЛБК: скалярное произведение любой кодовой комбинации на проверочный вектор равно нулю.
Обозначим проверочный вектор через h=(h1, h2….hn), а кодовую комбинацию через v=(v1, v2,…,vn), тогда их скалярное произведение равно 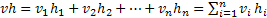 .
.
Сумма берется по всем слагаемым, в которых hi=1, т.е. сводится к сумме элементов кодовой комбинации, охваченных проверкой на четность, а потому эта сумма должна быть равна 0.
Записывая проверочные векторы в прямоугольную таблицу, получим проверочную матрицу кода, обозначаемую H(n,k) и имеющую размерность (n-k)×k.
Единицы на позициях, соответствующих информационным элементам в кодовой комбинации, указывают на то, какие информационные элементы участвуют в формировании проверочного элемента, а единица на позициях избыточных элементов указывает, какой именно проверочный элемент образован данной суммой информационных элементов.
Для порождающей и проверочной матриц справедливо равенство
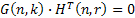 [3]
[3]
Решение данного матричного уравнения позволяет определить вид проверочной матрицы. Проверочная матрица формируется следующим образом – в начале строится единичная матрица Ek,r,
после чего к ней приписывается матрица Bk,r, содержащая k столбцов и r строк, причем каждая ее строка соответствует столбцу проверочной подматрицы Br,k порождающей матрицы, т.е. 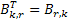
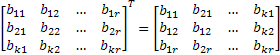
В результате проверочная матрица имеет вид:
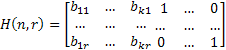 [5]
[5]
Или 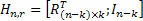 , где In-k - единичная матрица размерности (n-k)×(n-k).
, где In-k - единичная матрица размерности (n-k)×(n-k).
Введение проверочной матрицы позволяет нормализовать процесс вычисления проверочных соотношений для любой кодовой комбинации, сведя ее к произведению кодовой комбинации на проверочную матрицу по следующему правилу:
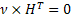 [6]
[6]
Т.е. некоторая комбинация ν принадлежит (n-k)-коду тогда и только тогда, когда она ортогональна каждой строке матрицы H(n,k). Соотношение [6] лежит в основе процедуры декодирования для ЛБК.
В результате умножения принятой комбинации на проверочную матрицу получаем вектор из (n-k) символов, называемый синдромом.
В случае, если синдром нулевой, то кодовая комбинация считается принятой безошибочно. В противном случае фиксируется наличие ошибок в кодовой комбинации.
Задача декодирования может быть решена следующим образом:
1. Определяются виды синдромов для возможных вариантов искажений кодовых комбинаций.
2. В декодере производится расчет синдрома.
3. Производится определение позиции ошибки, соответствующей рассчитанному синдрому.
4. Производится коррекция кодовой комбинации.
 2015-05-06
2015-05-06 2156
2156
