В настоящее время широкое распространение получил подкласс циклических кодов – коды БЧХ. Эти коды позволяют исправлять как независимые, так и пачки ошибок кратностью tu.
Идея построения кодов БЧХ принципиально не отличается от общей идеи построения циклических кодов – код строится на основе линейной свертки простого кода и образующего полинома. В качестве образующего полинома выбирается произведение (наименьшее общее кратное) наиболее простых неприводимых полиномов, так называемых примитивных многочленов нечетного порядка, т.е.
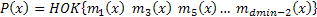 (5.9)
(5.9)
Такой полином позволяет получить большее количество остатков по сравнению с одиночным неприводимым многочленом, и, следовательно, коды при этом обладают лучшей корректирующей способностью.
Длина кодовой комбинации кодов БЧХ определяется:
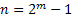 (5.10)
(5.10)
Длина кода БЧХ может быть равна 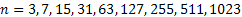 и т.д.
и т.д.
Количество проверочных разрядов кода:
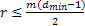 , (5.11)
, (5.11)
а число информационных разрядов:
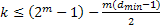 , (5.12)
, (5.12)
Пример. Пусть необходимо построить код длинной 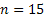 (
(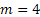 ) с
) с 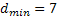 . Следовательно, образующий полином
. Следовательно, образующий полином 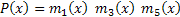 .
.
По таблице находим минимальные полиномы:
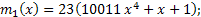
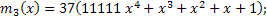
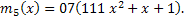
Перемножив полиномы, получим: 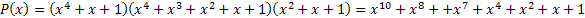 .
.
 2015-05-06
2015-05-06 524
524








