а) Основные определения и понятия.
Обобщенной спектральной теорией называют совокупность методов представления сигналов в виде суммы ортогональных составляющих
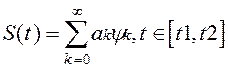 (1)
(1)
Наибольшее распространение получили методы, использующие представления сигналов в виде колебаний (т.е. функций времени) и спектрального разложения на синусоидальные и косинусоидальные составляющие (это преобразования Фурье). Обобщенная спектральная теория исследует общие закономерности спектрального анализа для систем базисных функций и рассматривает особенности выбора базисных систем при решении задач передачи и обработки сигналов. Представление (1) называют разложением сигнала по системе базисных функций. К системе базисных функций предъявляют следующие требования: для любого сигнала ряд (1) должен сходиться; функции 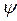 к(t) должны иметь простую аналитическую форму; коэффициенты ак должны вычисляться относительно просто. Этим трем условиям удовлетворяют системы ортогональных функций. Условие ортогональности функций
к(t) должны иметь простую аналитическую форму; коэффициенты ак должны вычисляться относительно просто. Этим трем условиям удовлетворяют системы ортогональных функций. Условие ортогональности функций
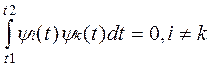 (2)
(2)
При i=k
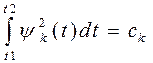 (3)
(3)
Число ck называют нормой базисной функции 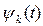 . Нормированная базисная функция
. Нормированная базисная функция
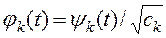 (4)
(4)
Система нормированных базисных функций 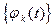 , удовлетворяющая одновременно и условию ортогональности, и условию нормировки
, удовлетворяющая одновременно и условию ортогональности, и условию нормировки
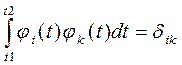 (5)
(5)
где 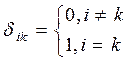 ,
,
называется ортонормированной.
Если под yi или yk понимать ток или напряжение, то равенство (3) имеет смысл энергии сигнала, выделенной сигналом yk на сопротивлении 1 Ом за время (t2-t1), а равенство (2) имеет смысл энергии взаимодействия сигналов yi и yk. Отсюда следует физический смысл понятий ортогональности и нормы функций: ортогональные сигналы не взаимодействуют между собой, а энергия нормированного сигнала равна 1.
б) Определение коэффициентов.
Рассмотрим, как определяют коэффициенты ак при разложении сигнала по системе ортонормированных функций. Представим сигнал
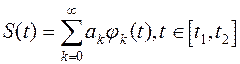 (6)
(6)
Умножив обе части (6) на ji(t) и проинтегрировав на интервале [t1,t2] получим
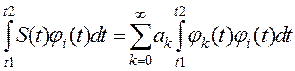 (*)
(*)
Из условия ортонормированности функций (5) следует, что в правой части соотношения (*) все интегралы при i¹k будут равны нулю, а при i=k один из них равен единице. Поскольку знак суммы в правой части (*) при этом исчезает, то
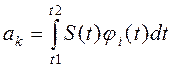 (7)
(7)
Ортогональные разложения (6) называют обобщенным рядом Фурье, а коэффициенты (7) - обобщенным коэффициентом Фурье.
Ортонормированные функции удовлетворяют трем условиям: они должны иметь простую аналитическую форму; для любого сигнала ряд должен сходиться; коэффициенты ak должны вычисляться относительно просто.
Выбор базисных ортонормированных функций - одна из ответственных задач и ее решение существенно зависит от характера преобразований сигналов в системе. Коэффициенты ak представляют собой эффективные значения составляющих спектра (обобщенных гармоник), поэтому выделяемая на сопротивлении 1 Ом средняя мощность сигнала равна:
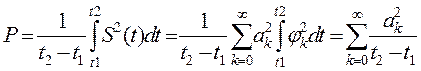 (8)
(8)
Соотношение (8) называют равенством Парсеваля. Из него следует, что мощность сигнала равна сумме мощностей всех составляющих спектра.
в) Минимизация погрешности разложения.
Определим коэффициенты, минимизирующие погрешность ортогонального разложения. Используем для этого понятие среднеквадратичной погрешности:
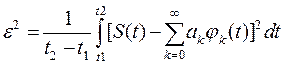 (9)
(9)
Для минимизации 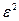 необходимо решить систему уравнений вида
необходимо решить систему уравнений вида
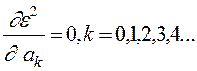 (**)
(**)
Для этого, при условии 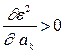 необходимо найти из решения akопт, подставить значения этих коэффициентов в (9) и определить
необходимо найти из решения akопт, подставить значения этих коэффициентов в (9) и определить
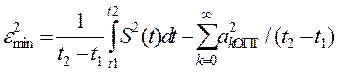 (10)
(10)
Эту задачу решил Фурье. Он показал, что оптимальными будут коэффициенты, определяемые по соотношению (7); если число членов ряда n< 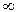 , то имеется некоторая среднеквадратическая погрешность, из-за которой
, то имеется некоторая среднеквадратическая погрешность, из-за которой
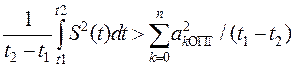 и
и 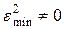 (11)
(11)
если же n® 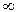 , то это неравенство выраждается в равенство Парсеваля (8) и, следовательно,
, то это неравенство выраждается в равенство Парсеваля (8) и, следовательно, 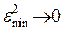 .
.
Таким образом, бесконечный ряд дает адекватное в среднеквадратическом смысле ортонормированное разложение сигнала.
г) Выбор числа членов ряда.
Для реальных сигналов всегда можно указать такое число n (обычно небольшое), при котором 80...... 90% мощности заключено в составляющих спектра с номерами n³k. Поэтому ряды, используемые на практике, конечны, а число членов ряда определяет допустимые среднеквадратические погрешности. Относительную погрешность разложения определяют как отношение DR(n) ошибки аппроксимации к мощности Р самого сигнала:
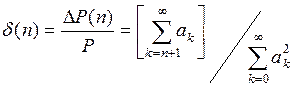 (12)
(12)
Ошибка аппроксимации, т.е. величина DR(n) - это та часть мощности, которая оказывается за пределами используемой полосы частот и не учитывается при восстановлении сигнала. По допустимой относительной погрешности d0 из соотношения d(n)= d0 нетрудно определить число n удерживаемых членов ряда.
д) Базисные сигналы.
В качестве базисных используют системы ортогональных функций Бесселя, Хаара, Уолша, системы ортогональных полиномов Лежандра, Чебышева, Эрмита, Лаггера и др. Примеры ортогональных разложений по таким функциям рассмотрим позднее. Реальные сигналы всегда ограничены во времени и имеют неограниченный спектр. Для удобства изучения сигналы часто рассматривают не на конечном интервале времени [t1,t2], а на полубесконечном [0, 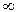 ] или на бесконечном [-
] или на бесконечном [- 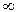 ,
, 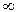 ]. Для определенности начало отсчета совмещают с началом сигнала или с серединой. Если сигнал имеет конечную длительность, то его рассматривают на интервале [0,T] или [-T/2,T/2].
]. Для определенности начало отсчета совмещают с началом сигнала или с серединой. Если сигнал имеет конечную длительность, то его рассматривают на интервале [0,T] или [-T/2,T/2].
Реальные сигналы случайны. Несмотря на это в теории часто рассматривают сигналы, полностью известные в любой момент. Такие сигналы называют детерминированными. Теория детерминированных сигналов, как теория первого приближения, удобна для решения простейших задач и полезна для развития теории случайных процессов.
е) Взаимная энергия и взаимная мощность.
Для изучения взаимосвязей сигналов используют два основных понятия: - взаимная энергия сигналов S1(t) и S2(t)
E12= 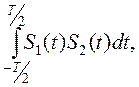 (13)
(13)
- взаимная мощность сигналов S1(t) и S2(t)
P12= 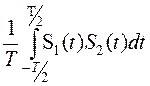 (14).
(14).
ж) Условия ортогональности и когерентности.
Различают сигналы ортогональные по энергии, когда E12=0 и ортогональные по мощности, когда P12=0. Для ортогональных сигналов средняя мощность и энергия суммы обладают свойством аддитивности (т.е. значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям при любом разбиении объекта на части). Это свойство записывается в виде соотношений:
P= 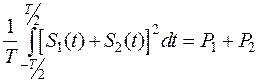
E= 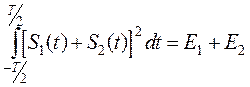 .
.
Сигналы, ортогональные по мощности, образуют более широкий класс, частью которого являются сигналы ортогональные по энергии, поскольку первые привязаны к конечным интервалам времени.
Из ортогональности по энергии следует ортогональность по мощности, но не наоборот, поскольку понятие ортогональности по энергии является более общим. Только на конечном интервале времени T< 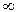 условия ортогональности по мощности и по энергии выполняются одновременно. Следовательно, ортогональность сигналов тесно связана с интервалом их определения.
условия ортогональности по мощности и по энергии выполняются одновременно. Следовательно, ортогональность сигналов тесно связана с интервалом их определения.
Взаимные энергия и мощность характеризуют степень сходства сигналов. Если два сигнала полностью совпадают, то P12=P21=P, где Р - мощность любого из сигналов (S1 или S2).
Такие сигналы называются полностью когерентными. Для ортогональных по мощности сигналов P12=P21=0, следовательно ортогональные сигналы полностью некогерентны. Если 0<P12<P или 0<P21<P, то сигналы называют частично - когерентным.
з) oртогональность постоянной и переменной составляющих.
Большое значение имеет ортогональность постоянной S0 и переменной S1,n составляющих любого сигнала S(t)=S0+ S1,n(t), где постоянная составляющая определяется как среднее значение сигнала на интервале [0,T]-S0= 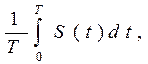 а переменная составляющая S1,n(t)=S(t)-S0.
а переменная составляющая S1,n(t)=S(t)-S0.
Взаимная энергия постоянной и переменной составляющих
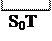
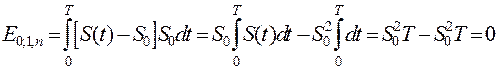 .
.
Следовательно, составляющие S0 и S1,n, ортогональны. Из их ортогональности следует, что среднее значение переменной составляющей
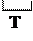
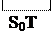
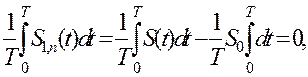
и что их прохождение через различные цепи может рассматриваться отдельно, а результат определяться простым суммированием.
 2015-05-06
2015-05-06 2332
2332
