Под статистической независимостью двух случайных величин 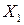 и
и 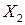 понимается, что плотность вероятности одной случайной величины не зависит от того, какое значение принимает другая величина. В таком случае двумерная плотность вероятности представляет собой произведение одномерных плотностей вероятностей:
понимается, что плотность вероятности одной случайной величины не зависит от того, какое значение принимает другая величина. В таком случае двумерная плотность вероятности представляет собой произведение одномерных плотностей вероятностей:
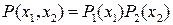 ,
,
что определяет условие статистической независимости.
При наличии статистической связи между случайными величинами статистические свойства каждой из них зависит от значения, принимаемого другой величиной.
Мерой линейной статистической связи между случайными величинами является коэффициент корреляции:
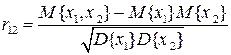
При этом 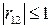 . Предельные значения
. Предельные значения 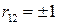 достигаются, если реализации случайных величин
достигаются, если реализации случайных величин 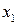 и
и 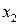 жестко связаны линейным соотношением вида
жестко связаны линейным соотношением вида 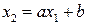 , причём знак коэффициента и определяет знак
, причём знак коэффициента и определяет знак 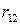 .
.
Отсутствие линейной статистической связи означает отсутствие коррелированности случайных величин 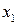 и
и 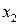 . При этом
. При этом 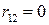 .
.
Таким образом для некоррелированных случайных величин:
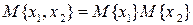
Из статистической независимости следует некоррелированность двух случайных величин. Обратное неверно, т.е. некоррелированные случайные величины могут быть зависимыми.
Пример.
Случайные величины 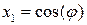 и
и 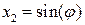 , где
, где 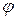 – случайная величина. Очевидно, что
– случайная величина. Очевидно, что 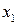 и
и 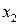 являются статистически зависимыми, однако,
являются статистически зависимыми, однако, 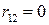 .
.
 2015-05-06
2015-05-06 845
845








