В ряде случаев оказывается более удобным в качестве базисов разложения использовать такие системы функций, для которых коэффициенты разложения учитывают поведение исходной функции лишь в нескольких близкорасположенных точках.
Использование такого базиса по своей сути означает переход от частотного анализа к масштабному, т.е. функция f(x) анализируется с помощью некоторой “стандартной” математической функции, изменяемой по масштабу и сдвигу на некоторую величину.
Первое упоминание об этих функциях появилось в работах Хаара в 1909 году. В 30-е годы начались более детальные исследования возможностей представления сигналов с использованием базисных масштабируемых функций. Пол Леви, используя масштабируемую базисную функцию типа функции Хаара, исследовал разновидность случайного сигнала - броуновское движение. Он обнаружил преимущество в применении базисных функций Хаара перед функциями Фурье.
В период 60-х - 80-х годов Вейс и Кофман исследовали простейшие элементы функционального пространства, названные ими атомами, с целью обнаружить атомы для произвольной функции и найти "правила сборки", позволяющие реконструировать все элементы функционального пространства, используя эти атомы. В 1980 году Гроссман и Марлет определили такие функции как Wavelet-функции. В переводе с английского Wavelet – всплеск, поэтому в отечественной литературе встречается термин «разложение по всплескам» наряду с вейвлет-анализом.
В конце 80-х г.г. Мейер и Добичи на основе исследований Марлета создали ортогональные базисы Wavelet-функций, которые и стали основой современных Wavelet-функций. Сходство Wavelet и Фурье преобразований состоит в следующем:
1. Оба они являются линейными преобразованиями и предназначены для обработки блоков данных, содержащих log2 N элементов.
2.Обратные матрицы ДПФ и DWT (discret wavelet transform) равны транспонированной, причем строки самих матриц содержат функции cos(x) и sin(x), а для DWT - более сложные базисные функции - wavelet.
Наиболее важное различие между этими двумя видами преобразований состоит в том, что отдельные функции wavelet локализованы в пространстве, а синусные и косинусные - нет. Благодаря этой особенности, DWT находит большое число применений, в том числе для сжатия данных, распознавания образов и подавления шумовой составляющей принимаемого сигнала.
Преобразование Wavelet состоит из неограниченного набора функций. Семейство Wavelet различают по тому, насколько компактны базисные функции в пространстве и насколько они гладки. Некоторые их них имеют фрактальную структуру. В каждом семействе они могут быть разбиты на подклассы по числу коэффициентов и уровню итераций. Чаще всего внутри семейства функция классифицируется по номеру моментов исчезновения.
Набор дискретных Wavelet-функций в общем виде может быть описан как
W[s,l](x) = 2-s/2W(2-s,x-l), (7.2)
где s и l - целые числа, которые масштабируют и сдвигают материнскую функцию W(x) для создания wavelet.
Индекс масштаба s показывает ширину wavelet, а индекс смещения l определяет ее позицию. Материнские функции масштабированы или растянуты коэффициентом, кратным степени 2 и приведены к целому. Таким образом, если известна материнская функция, то может быть построен и весь базис.
В свою очередь, само Wawelet-преобразование может быть записано в виде [2,26]:
N-2
V(x) = ∑(-1)k zk+l W(2x+l) (7.3)
k=1
где Zk+l – отсчеты исходного сигнала.
Метод разложения по всплескам широко используется для выделения шумовой компоненты при обработке данных.
К wavelet-подобным функциям относятся функции Хаара [6]. Для N=4 и N=8 матрицы ядра преобразования имеют вид:
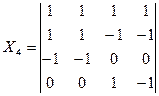
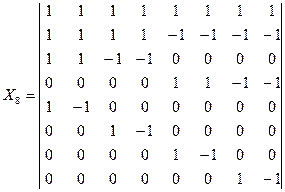
Основные свойства матрицы ядра преобразования Хаара состоят в следующем:
а) ее элементы не мультипликативны
б) матрица не симметрична, откуда следует, что для обратного преобразования матрицу ядра необходимо транспонировать, т.е.
XN-1 = XNT
в) строки матрицы определяют переодические функции с периодом N.
Однако матрица ядра преобразования Хаара является не ортонормированной, т.е. для данного преобразования не выполняется теорема Парсеваля. Поэтому для выполнения теоремы Парсеваля требуется ввести дополнительную нормировку, такая нормировка заключается в умножении на Ö2 тех элементов вектора результатов, которые соответствуют строкам матрицы с нулевыми компонентами. Для строк, содержащих N/2 ненулевых элемента такое умножение выполняется один раз, для строк с N/4 ненулевыми элементами - два раза и так далее. Подобную нормировку необходимо выполнять как при выполнении прямого, так и обратного преобразования Хаара.
Близким к преобразованию Хаара является усеченное преобразование Адамара, отличающееся, по своей сути, лишь порядком следования строк матрицы ядра преобразования [6].
 2015-05-06
2015-05-06 827
827







