Вейвлеты

В математической теории сигналов принято считать, что сигналы определены как векторы в некотором пространстве V. Бесконечно размерное пространство, часто используемое в теории вейвлетов, называется гильбертовым пространством L²[R]. Вейвлет функции Y, принадлежащие L²[R] должны иметь нулевое среднее значение и затухать на бесконечности. Ввиду ограниченности действия вейвлетов, они могут покрывать всю вещественную ось, если обладают возможностью сдвига по этой оси, а также свойством масштабирования, которое можно уподобить изменению частоты гармоник в рядах Фурье. Обладая этими свойствами, вейвлеты позволяют представить локальные особенности сигналов [1,3,12,13,16,19].

На основании понятий о векторном пространстве общим подходом к анализу сигналов s(t) стало их представление в виде взвешенной суммы простых составляющих – базисных функций Y_k(t), умноженных на коэффициенты C_k:

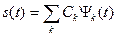(7.4)

Термин вейвлет, введён впервые Морле, в переводе с английского означает «короткая волна» или «всплеск». Грубо вейвлеты можно представить как некоторые волновые функции, способные осуществлять преобразование Фурье не по всей временной оси, а локально по месту своего расположения. Базисными функциями вейвлетов могут быть различные функции, в том числе, напоминающие модулированные импульсами синусоиды, функции со скачками уровня и т.д. Это обеспечивает лёгкое представление сигнала со скачками и разрывами.

Вейвлеты характеризуются своими временными и частотными образами. Временной образ представляет собой некую функцию Y(t) времени, а частотный образ определяется её Фурье-образом: .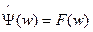

Таким образом, с помощью вейвлетов сигнал представляется совокупностью волновых пакетов, образованных на основе некоторой исходной базовой функции Y₀(t). Эта совокупность, разная в различных частях временного интервала определения сигнала и корректируемая множителями, и представляет с той или иной степенью детализации. Такой подход называют вейвлет анализом сигналов.

Число используемых вейвлетов, при разложении сигнала, задаёт уровень декомпозиции сигнала. За нулевой уровень декомпозиции часто принимают сам сигнал, а последующие уровни декомпозиции образуют ниспадающее вейвлет дерево.

Одна из основополагающих идей вейвлет-представления вейвлет представлении сигнала заключается в разбивке приближения сигнала на две составляющих: грубую (аппроксимирующую) и приближенную (детализирующую), с последующим их уточнением итерационным методом. Каждый шаг такого уточнения соответствует определённому уровню декомпозиции и реставрации сигнала.

Как и преобразование Фурье, вейвлет преобразования можно применять как к непрерывным сигналам – непрерывные вейвлет преобразования, так и к цифровым сигналам – дискретные вейвлет преобразования.