2015-05-06
356
В большинстве приложений работа осуществляется с дискретными сигналами. Поэтому представляют интерес дискретные аналоги НВП, которые преобразуют дискретный сигнал в непрерывный и дискретный сигналы, соответственно.
Пусть имеется некоторая непрерывная функция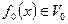 
. Дискретный сигнал 
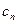представим как последовательность коэффициентов при масштабирующих функциях, по которым раскладывается 
:
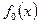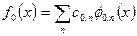, (7.10)
где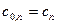 
.
Другими словами, сигнал интерпретируется как последовательность коэффициентов разложения, полученную в ходе кратномасштабного анализа функции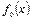 
. Тогда можно вычислить аппроксимацию этой функции, принадлежащие пространствам 
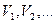. Пространства 
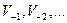не имеют значения при данной интерпретации.
Согласно концепции кратномасштабного анализа функция 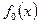декомпозируется на две функци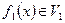и 
и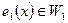 
:
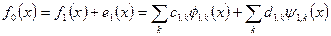. (7.11)
Таким образом, получили две новые последовательност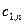и 
и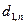 
. Этот процесс может быть продолжен по 
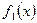, и функция 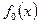(а также и последовательность 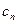) будет представлена совокупностью коэффициентов 
.
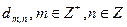Рассмотрим, как вычисления ДВП могут быть выполнены с использованием операций только над дискретными сигналами. С учетом того, что масштабирующая функция образует базис соответствующего пространства, можно получить
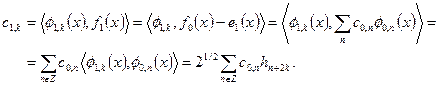(7.12)
Отсюда оказывается возможным итеративное вычисление коэффициентов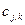 
и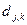 
без непосредственного использования функци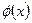й 
и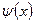 
.
.
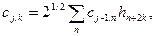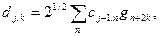(7.13)
получив, таким образом, полностью дискретный процесс декомпозиции. Последовательност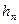и 
и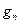 
называются фильтрами. Следует отметим, что 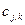и 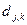имеют «половинную» длину по сравнению с 
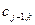. За счет этого не вводится избыточности.
Обратный процесс заключается в получении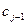 
из 
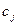и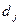 
:
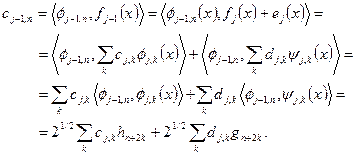(7.14)
Длина последовательности 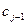вдвое больше длины последовательност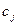и или .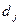
Для фильтров 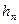и 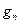существуют следующие ограничения:
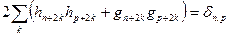, (7.15)
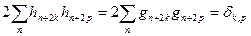, (7.16)
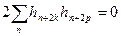. (7.17)
