Вычислительная сложность ДПФ и способы её сокращения

Во второй главе мы пришли к выводу, что любое ортогональное преобразование в матричной форме может быть описано как процедура умножения вектора исходных данных на матрицу ядра (при прямом преобразовании)

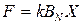
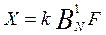или вектора результатов разложения исходного сигнала по тем или иным базисным ортогональным функциям на обратную матрицу (при обратном преобразовании):

В общем случае вычислительная сложность такой процедуры составляет

Q = N²(БО),

где отдельная базовая операция включает операцию умножения и сложения действительных чисел или те же операции умножения и сложения, но для комплексных чисел, в случае преобразования Фурье. С учётом того, что для комплексных чисел

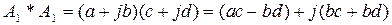
сложность вычислительной процедуры ДПФ

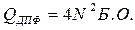, (8.1)

если под Б.О. понимать те же операции, как и в базисах действительных функций.

В целях сокращения объёма вычислений можно выполнить формирование отсчётов вектора 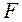с учётом вырождения (т.е. тривиальности) первой строки и первого столбца матрицы ДПФ:

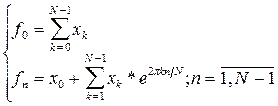(8.2)

Отметим особенности представления чётных и нечётных функций при ДПФ и ДПХ. Пусть исходный сигнал описан как суперпозиция чётной и нечётной составляющей:

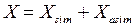
причем для каждой из составляющих можно записать

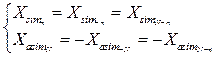(8.3)

С учётом такого представления сигнала можно записать, что

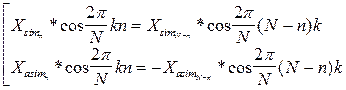(8.4а)

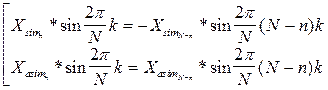(8.4б)

поэтому для чётного исходного сигнала “синусная” компонента спектра будет равна 0, а для нечётного сигнала - “косинусная” компонента спектра равна 0.

Поэтому спектр действительного сигнала в базисах Фурье и Хартли описывается чётной функцией и для его задания требуется только косинусная компонента, причём в силу чётности для задания спектра достаточно только 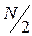отсчётов .

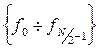Кроме того, матрицы 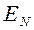и 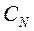обладают свойством симметрии и периодичности (цикличности) следования элементов. Из симметрии матриц указанных ядер следует, что в общем случае для действительных последовательностей (т.е. вектора 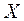, содержащего только действительные элементы) может быть выполнено только для 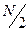компонент спектра, (например, с номерами 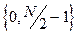), поскольку компоненты “положительной” и “отрицательной” областей частот (компоненты с номерам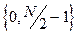и и 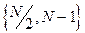имеют одинаковую амплитуду, но противоположные фазы. Поэтому вторую половину компонент можно легко достроить из вычисленных.

Аналогично можно поступить и при вычислении ДПХ - cos-составляющая “положительных” и “отрицательных” спектральных компонент одинакова, а sin-составляющие для “положительных” и “отрицательных” имеют противоположные знаки.