Запись алгоритма БПФ в векторно-матричной форме

Матрицы указанных ортогональных преобразований позволяют значительно сократить объём вычислений, поскольку из 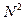элементов матрицы имеется лишь 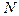(для ДПФ и ДПХ) различных значений.

Действительно, рассмотрим ДПФ для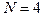

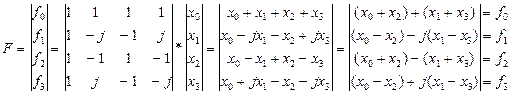
После выделения встречающихся неоднократно блоков данных можно заметить, что 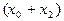и 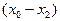есть не что иное, как ДПФ для 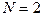и подвектора 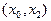. Аналогичные выводы можно сделать и для других блоков данных, что позволяет записать:

;

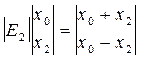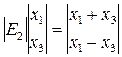
Попробуем использовать как типовой элемент преобразования процедуру вида 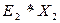и перекомпоновку векторов.

1) Переставим элементы исходного вектора, чтобы сформировать указанные подвектора. Очевидно, что для такой перестановки необходимо двоично-инверсное переупорядочивание вектора .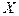

Такая процедура может быть записана как операция умножения вектора 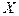на перестановочную матрицу .

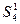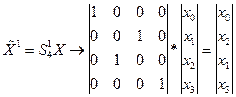
2) Запишем матрицу

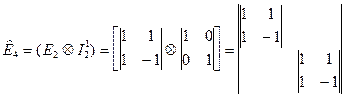
и получим вектор 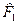как:

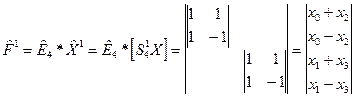
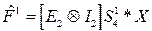
3) Умножим вектор 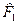на диагональную матрицу :

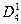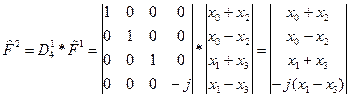
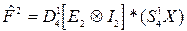
4) Получим вектор 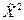, вновь переставив элементы вектора 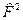по правилу двоичной инверсии с помощью матрицы :

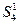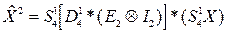
5) Умножим вектор 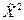на матрицу :

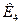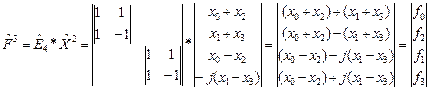
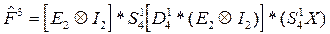
6) Переставим элементы вектора 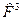с помощью матрицы :

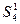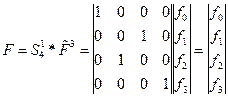
иначе говоря:

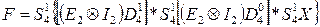(8.5)

где на первой итерации диагональная матрица

введена формально, для симметрии матричной записи обоих итераций.

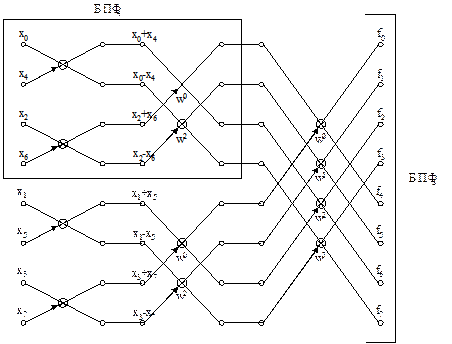
Рассуждая аналогичным образом, можно придти к алгоритму, состоящему в выполнении последовательности итераций. На рис.8.1 приведен граф алгоритма БПФ, иллюстрирующий выполнение итеративнно - связанных вычислений по описанной схеме.

Рис.8.1. Граф процедуры БПФ для N = 8.

На рисунке обозначены:

; ; ;

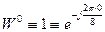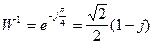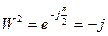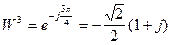
Число итераций составляет 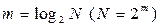. Перед первой итерацией выполняется r-ично инверсная перестановка элементов вектора исходных данных. В свою очередь каждая итерация сводится к схожим действиям:

1. Перестановка элементов вектора результатов предшествующей итерации;

2. Умножение вектора данных на диагональную матрицу 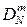(m - номер итерации), причём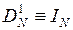

3. Умножение вектора результатов (по п.1) на матрицу блочной структуры

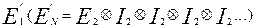4. Выполнение перестановок элементов вектора, содержащего результаты п.2.

В матричном виде это можно записать [6, 11,25]:

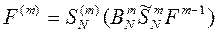(8.6),

где 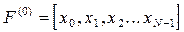- вектор исходных данных,

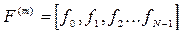- вектор результатов БПФ,

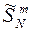- матрица перестановок вектора выходных данных (т.е. ),

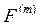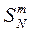- матрица перестановок вектора входных данных (т.е. ).

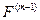В свою очередь, матрица 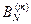является блочной матрицей, процедура формирования которой определяется выражением:

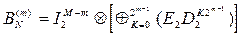(8.7),

здесь 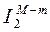- единичная матрица порядка ,

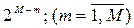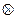- знак прямого произведения матриц (кронекеровского произведения),

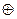- знак прямой суммы матриц. Заметим, что прямой суммой матриц 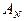и 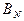является диагональная матрица 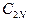на главной диагонали которой расположены блоки из исходных матриц:

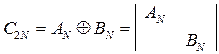(8.8).

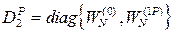- диагональная матрица поворачивающих множителей (),

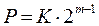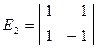- матрица ДЭФ порядка,

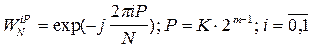
Такое представление алгоритма БПФ в виде матричных операций носит в большей мере характер формального описания. Действительно, выполнение перестановок как операций умножения вектора на матрицу явно не является оптимальным путем их реализации, также как и описываемые через аналогичные операции умножения на поворачивающие множители.

Серьезным недостатком такого представления алгоритма БПФ является трудность перехода к программной реализации алгоритма.

Для практических целей более удобно описание алгоритма БПФ через систему рекуррентных выражений.