Формулировка теоремы: производная по времени от кинетического момента системы относительно неподвижной оси 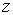 равна сумме моментов всех внешних сил относительно этой оси, т. е.
равна сумме моментов всех внешних сил относительно этой оси, т. е.
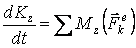 . (2.4)
. (2.4)
Рассмотрим методику решения задач с помощью этой теоремы:
– изображаем систему в произвольный момент времени, показывая все внешние силы, действующие на систему;
– находим сумму моментов внешних сил относительно оси;
– находим кинетический момент системы относительно оси;
– находим производную по времени от кинетического момента системы;
– составляем уравнение (2.4);
– решаем это уравнение, находим искомые величины.
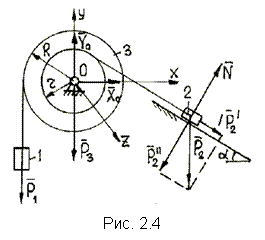
Задача 2.1 (11). Грузы 1 и 2 весом 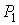 и
и 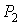 прикреплены к концам тросов, навернутых на ступенчатый барабан 3 весом
прикреплены к концам тросов, навернутых на ступенчатый барабан 3 весом 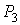 с радиусами
с радиусами 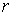 и
и 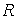 (рис. 2.4), момент инерции барабана
(рис. 2.4), момент инерции барабана 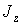 задан. Определить, пренебрегая трением и весом тросов, закон изменения угловой скорости барабана 3.
задан. Определить, пренебрегая трением и весом тросов, закон изменения угловой скорости барабана 3.
Решение
Внешние силы 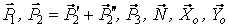 .
.
Находим сумму моментов внешних сил относительно оси 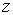
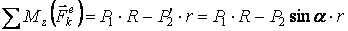 ,
учитывая при этом, что силы ,
учитывая при этом, что силы 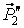 и и 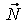 взаимно уравновешиваются, а моменты сил взаимно уравновешиваются, а моменты сил 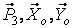 относительно оси относительно оси 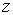 равны нулю.
Находим равны нулю.
Находим 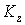 данной системы данной системы
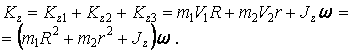 Находим производную по времени от
Находим производную по времени от 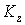
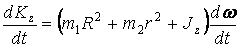 . .
| 
|
Уравнение (2.4) представим в виде 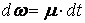 ,
,
где 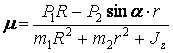 .
.
Интегрируя это дифференциальное уравнение, получим
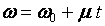 ,
,
где 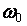 – угловая скорость барабана 3 в начальный момент.
– угловая скорость барабана 3 в начальный момент.
 2015-05-06
2015-05-06 663
663








