1) выделить механическую систему, движение которой рассматривается;
2) выявить все активные силы изобразить их приложенными к механической системе на чертеже;
3) освободить систему от связей и заменить их реакциями связей;
4) добавить к полученной системе сил силы инерции и моменты сил инерции;
5) записать уравнения равновесия полученной системы сил и определить искомые величины.
Пример решения задач по теме:
С вертикальным валом АВ, вращающимся с постоянной угловой скоростью ω, жестко скреплен стержень OD длиной l и массой m1, имеющий на конце груз массой m2 (Рис. 8)
Дано:
b1=0.6м, b2 =0,2м, l=0,5м, α=30о, m1=3кг, m2=2кг, ω= 6с-1.
Определить реакции подшипника В и подпятника А.
Расчетная схема имеет вид:
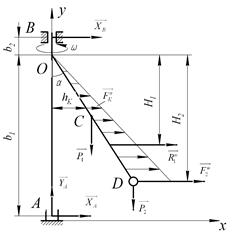
Рис.8
Решение:
Для определения искомых реакций рассмотрим движение механической системы, состоящей из вала АВ, стержня OD и груза, применим принцип Даламбера. Проведем вращающиеся вместе с валом оси Аxy так, чтобы стержень лежал в плоскости xy, и изобразим действующие на систему внешние силы: силы тяжести Р1 и Р2, составляющие XА, YА, реакции подпятника и реакцию XВ подшипника.
Согласно принципу Даламбера присоединим к этим силам силы инерции элементов стержня и груза, считая груз материальной точкой. Так как вал вращается равномерно, то элементы стержня имеют только нормальные ускорения, направленные к оси вращения, а по модулю они равны
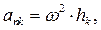 где
где 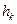 - расстояние элемента от оси. Тогда силы инерции будут направлены от оси вращения и по модулю будут равны:
- расстояние элемента от оси. Тогда силы инерции будут направлены от оси вращения и по модулю будут равны:
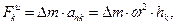 где
где 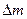 - масса элемента.
- масса элемента.
Поскольку все 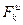 пропорциональны
пропорциональны 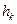 , то эпюра этих параллельных сил образует треугольник и их можно заменить равнодействующей
, то эпюра этих параллельных сил образует треугольник и их можно заменить равнодействующей 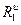 , линия действия которой проходит через центр тяжести этого треугольника, т.е. на расстоянии H1 от вершины О, где
, линия действия которой проходит через центр тяжести этого треугольника, т.е. на расстоянии H1 от вершины О, где 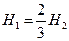 , (
, (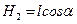 ).
).
Как известно равнодействующая любой системы сил равна ее главному вектору, а по модулю главный вектор сил инерции стержня R1и=m1ac где ас – ускорение центра масс стержня; при этом, как и для любого элемента стержня, ac= 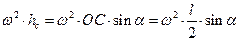 . В результате получим:
. В результате получим:
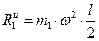 =3
=3 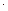 36
36 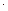 0,25
0,25 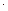 0,5=13,5 Н.
0,5=13,5 Н.
Аналогично для силы инерции F2и груза найдем, что она тоже направлена от оси вращения, а по модулю: 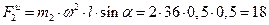 Н.
Н.
Так как все действующие силы и силы инерции лежат в плоскости xy, то и реакция подпятника А и подшипника В тоже лежат в этой плоскости, что было учтено при их изображении.
По принципу Даламбера, приложенные внешние силы и силы инерции образуют уравновешенную систему сил. Составляя для этой плоской системы сил три уравнения равновесия, получим:
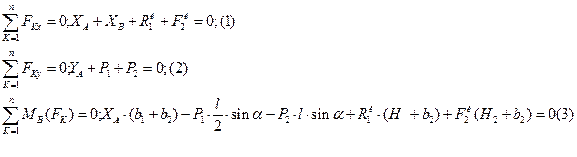
Подставив числовые значения всех заданных и вычисленных величин и решив эту систему уравнений, найдем искомые реакции.
Ответ: XA = 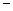 11,8 Н; YA =49,1H; XB=
11,8 Н; YA =49,1H; XB= 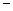 19,7 H/
19,7 H/
Знаки указывают, что силы XA и XB направлены противоположно показанным на рисунке 8.
 2015-05-06
2015-05-06 804
804








