Тема: Применение общего уравнения динамики к исследованию движения механической системы».
Механическая система под действием силы тяжести приходит в движение из состояния покоя, необходимо определить ускорения всех тел, входящих в систему. Массами нитей пренебречь. Трение качения и силы сопротивления в подшипниках не учитывать. Каток 3 – однородный цилиндр. Схема механической системы показана на рисунке 9.
Дано:
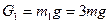 ;
; 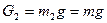 ;
; 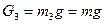 ;
; 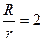 ;
; 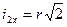 ; f=0,1.
; f=0,1.
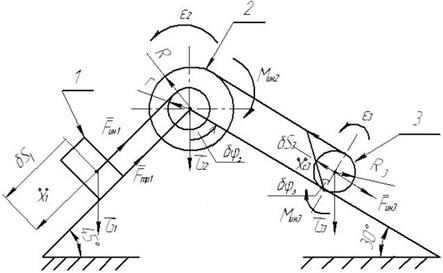
Рис.9
Решение:
Покажем на механической системе веса тел 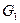 ,
, 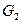 ,
, 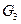 ; ускорения груза 1
; ускорения груза 1 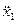 и центра цилиндра 3
и центра цилиндра 3 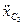 ; углы поворотов тел, совершающих вращательное движение
; углы поворотов тел, совершающих вращательное движение 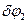 ,
, 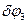 ; угловыеускорения
; угловыеускорения 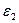 ,
, 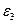 ; силу трения груза 1
; силу трения груза 1 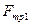 ; силы инерции
; силы инерции 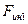 ,
, 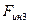 ; моменты сил инерции
; моменты сил инерции 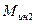 ,
, 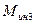 , как указано на рисунке 9.
, как указано на рисунке 9.
Используем общее уравнение динамики:
Если механическая система, на которую наложены голономные, стационарные, идеальные связи, движется с ускорением, то, добавляя к действующей на неё активным силам и моментам этих сил, фиктивные силы инерции и моменты сил инерции, получим формально уравновешенную систему сил, к которой можно применить принцип возможных перемещений.
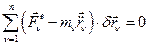 ; (1)
; (1)
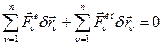 , (2)
, (2)
где 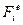 - внешние силы, действующие на систему;
- внешние силы, действующие на систему;
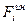 - силы инерции, действующие на систему;
- силы инерции, действующие на систему;
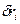 - возможное перемещение.
- возможное перемещение.
Запишем все уравнения связей для механической системы:
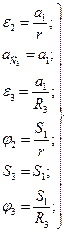 ; (3)
; (3)
где:
ε2, 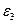 - угловое ускорение катка 3;
- угловое ускорение катка 3;
a1, ac3 - линейные ускорения груза 1 и центра однородного катка 3.
Так как система приходит в движение из состояния покоя, направления ускорения тел соответствуют направлениям движения тел.
Покажем все заданные силы и приложим силы и моменты инерции. Сила инерции груза 1, движущегося поступательно равна:
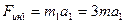 . (4)
. (4)
Сила инерции центра однородного цилиндра, центр которого движется поступательно, равна:
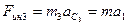 ; (5)
; (5)
Используя уравнение связи, определим момент сил инерции блока 2, совершающего вращательное движение:
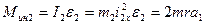 . (6)
. (6)
Используя (3) и (6), определим момент сил инерции однородного цилиндра 3, совершающего вращательное движение:
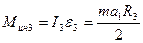 . (7)
. (7)
Сообщив механической системе возможное перемещение 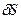 и возможный угол поворота
и возможный угол поворота 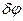 , составим общее уравнение динамики.
, составим общее уравнение динамики.
Так как
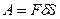 ; (8)
; (8)
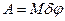 , (9)
, (9)
то общее уравнение динамики примет вид:
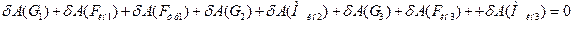
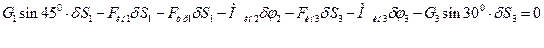 (11)
(11)
Учитывая уравнения (3) и исходные данные, полученные из условия задачи, получим:
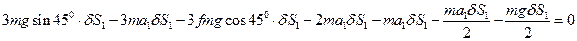 ;(12)
;(12)
Разделим каждое составляющее выражения на 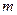 ,
, 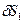 и выразим ускорение груза 1
и выразим ускорение груза 1 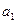 :
:
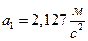 .
.
Для нахождения ускорений остальных тел воспользуемся уравнениями связи:
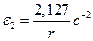 ;
;
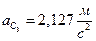 ;
;
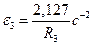 .
.
Результаты расчётов по данному методу представим в виде таблицы.
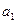 , , 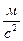
| 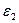 , , 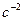
| 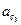 , , 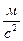
| 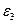 , , 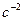
|
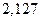
| 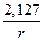
| 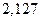
| 
|
 2015-05-06
2015-05-06 351
351








