Пример решения второй задачи движения. Движение точки, брошенной под углом к горизонту в однородном поле тяжести

Изучим движение тела, брошенного с начальной скоростью V₀ под углом α к горизонту, рассматривая его как материальную точку массы т. При этом сопротивлением воздуха пренебрежём, а поле тяжести будем считать однородным (Р=const), полагая, что дальность полёта и высота траектории малы по сравнению с радиусом Земли.

Поместим начало координат О в начальном положении точки. Направим ось Оy вертикально вверх; горизонтальную ось Ox расположим в плоскости, проходящей через Оy и вектор V₀, а ось Oz проведём перпендикулярно первым двум осям (рис.3). Тогда угол между вектором V₀ и осью Ox будет равен α.

Изобразим движущуюся точку М где-нибудь на траектории. На точку действует одна только сила тяжести 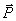, проекции которой на оси координат равны: Px=0, Py=-P=-mg, Pz=0.

Подставляя эти величины в дифференциальные уравнения и замечая, что 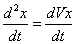и т.д. мы после сокращения на m получим:

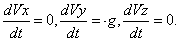
Умножая обе части этих уравнений на dt и интегрируя, находим:

Vx=C₁, Vy=-gt+C₂, Vz=c₃.

Начальные условия в нашей задаче имеют вид:

при t=0, x=0, y=0, z=0,

Vx=V­₀Cosα, Vy=V₀Sinα, Vz=0.

Удовлетворяя начальным условиям, будем иметь:

C₁=V₀Cosα, C₂=V₀Sinα, C₃=0.

Подставляя эти значения С₁, С₂ и С₃ в найденное выше решение и заменяя Vx, Vy, Vz на 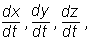придём к уравнениям:

.

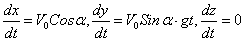Интегрируя эти уравнения, получим:

.

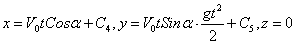Подстановка начальных данных даёт С₄=С₅=С₆=0, и мы окончательно находим уравнения движения точки М в виде:

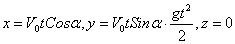(1)

Из последнего уравнения следует, что движение происходит в плоскости Оxy

Имея уравнение движения точки, можно методами кинематики определить все характеристики данного движения.

1. Траектория точки. Исключая из первых двух уравнений (1) время t, получим уравнение траектории точки:

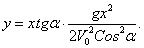(2)

Это - уравнение параболы с осью, параллельной оси Оy. Таким образом, брошенная под углом к горизонту тяжёлая точка движется в безвоздушном пространстве по параболе (Галилей).

2. Горизонтальная дальность. Определим горизонтальную дальность, т.е. измеренное вдоль оси Оx расстояние ОС=Х. Полагая в равенстве (2) y=0, найдём точки пересечения траектории с осью Ох. Из уравнения:

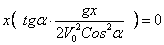
получаем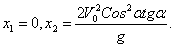

Первое решение дает точку О, второе точку С. Следовательно, Х=Х₂ и окончательно

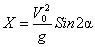. (3)

Из формулы (3) видно, что такая же горизонтальная дальность X будет получена при угле β, для которого 2β=180˚-2α, т. е. если угол β=90-α. Следовательно, при данной начальной скорости V₀ в одну и ту же точку С можно попасть двумя траекториями: на­стильной (α<45˚) и навесной (β= 90-α > 45˚).

При заданной начальной скорости V₀ наибольшая горизонтальная дальность в безвоздушном пространстве получается, когда sin2α=1, т. е. при угле α=45˚.

3. Высота траектории. Если положить в уравнении (2)

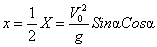, то найдется высота траектории Н:

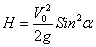. (4)

4. Время полета. Из первого уравнения системы (1) следует, что полное время полета Т определяется равенством x=V₀Tcos α. Заменяя здесь Х его значением, получим

.

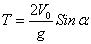При угле наибольшей дальности α=45˚ все найденные вели­чины равны:

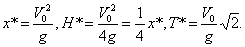
Полученные результаты практически вполне приложимы для ориен­тировочного определения характеристик полета снарядов (ракет), имеющих дальности порядка 200…600 км, так как при этих дальностях (и при α~45˚) снаряд основную часть своего пути проходит в стратосфере, где сопротивлением воздуха можно пренебречь. При меньших дальностях на результат будет сильно влиять сопротивле­ние воздуха, а при дальностях свыше 600 км силу тяжести уже нельзя считать постоянной.