| 1. Дифференциальный ворот состоит из двух цилиндров различного диаметра, закрепленных на общей оси. На цилиндрах укреплен канат, который при вращении ворота наматывается на цилиндр большего диаметра и сматывается с другого цилиндра. На образуемой канатом петле подвешен блок. Какую силу F нужно приложить к рукоятке ворота длиной l = 1 м, чтобы удерживать или равномерно поднимать груз, если радиусы цилиндров r1 = 0,2 м, r2 = 0,1 м, а сила тяжести груза Р = 100 Н? " | 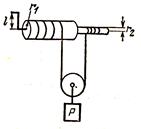
|
| 2. Пара одинаковых грузиков A и B, связанны нитью длины L, начинает соскальзывать c гладкого стола высоты l, причем в этот момент грузик B находится на высоте ВС=2l/3. Достигнув пола, грузик B прилипает к нему, сразу после чего грузик А слетает ее стола. На какой высоте у над уровнем пола окажется грузик A, когда нить вновь станет натянутой? | 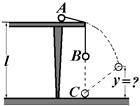
|
3. Груз массой 10 кг привязан к концу веревки, намотанной на лебедку. Груз и лебедка находятся на некоторой высоте. Груз начинает падать, причем веревка натянулась в тот момент, когда он пролетел 5 м. Вслед за этим начинает с трением раскручиваться лебедка. Какую минимальную длину веревки пришлось вытравить до полной остановки груза, если веревка выдерживает максимальную силу натяжения 147 Н?
4. На гладком столе лежат два одинаковых шара массой М каждый. Расстояние между шарами l намного больше их радиусов. В один из шаров по линии их центров попадает пуля массой m, летевшая горизонтально со скоростью v. Пробив первый шар, пуля теряет половину скорости и попадает во второй шар. Через сколько времени столкнутся шары?
5. Астронавты «Скайлэба» с помощью специального радиолокационного высотомера обнаружили, что поверхность океана в районе «Бермудского треугольника» ниже нормального уровня на 25 метров (см., например, журнал «Наука и жизнь», 1976, № 9). Предполагая, что этот «прогиб» можно объяснить наличием под дном океана шаровой полости, заполненной водой, оценить радиус этой полости. Глубина океана Н = 6 км.
6. Определить момент инерции J тонкой плоской пластины со сторонами а = 10 см и b = 20 см относительно оси, проходящей через центр масс пластины параллельно большей стороне. Масса пластины равномерно распределена по ее площади с поверхностной плотностью s = 1,2 кг/м3.
7. Маховик вращается по закону, выражаемому уравнением j = А + Вt + Сt2, где А == 2 рад; В = 16 рад/с; С = — 2 рад/с2. Момент инерции J колеса равен 50 кг×м2. Найти законы, по которым меняются вращающий момент М и мощность N. Чему равна мощность в момент времени t = 3 с?
8. Считая плотность Земли постоянной, определить, на какой глубине ускорение свободного падения составит 50% от его значения на поверхности.
9. Определить относительное удлинение алюминиевого стержня, если при его растяжении затрачена работа A=6,9Дж. Длина стержня l= 1 м, площадь поперечного сечения S= 1 мм модуль Юнга для алюминия E= 69 ГПа.
10. Выразить через кг, м, с размерность коэффициента вязкости.
 2015-05-06
2015-05-06 1769
1769








