Пусть, кроме силы упругости, на точку действует некоторая постоянная сила F (рис. 3). В этом случае основное уравнение динамики примет вид:
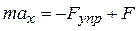 . (11)
. (11)
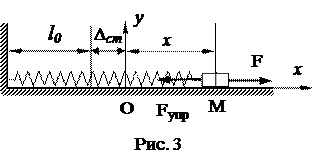 Выбрав начало координат в положении равновесия – т. О, имеем:
Выбрав начало координат в положении равновесия – т. О, имеем: 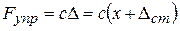 , где Δ ст – статическая деформация пружины под действием силы F.
, где Δ ст – статическая деформация пружины под действием силы F.
С учетом этого уравнение (11) примет вид: 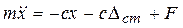 . Но
. Но 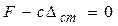 , тогда получим
, тогда получим 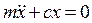 или
или
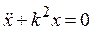 , (12)
, (12)
где 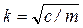 .
.
Сравнивая уравнения (4) и (12) видим, что они совпадают. Следовательно, совпадают и их решения. Таким образом, постоянная сила не изменяет характер колебаний точки, она лишь смещает центр колебаний в направлении действия силы на расстояние, равное статической деформации пружины.
По формуле (10): 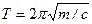 , учитывая, что
, учитывая, что 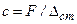 , имеем
, имеем 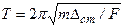 . Если постоянная сила является силой тяжести, то
. Если постоянная сила является силой тяжести, то 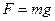 и период колебаний можно найти по формуле:
и период колебаний можно найти по формуле: 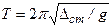 .
.
 2015-05-06
2015-05-06 1443
1443








