Замена системы упругих элементов одним – эквивалентным

Упругий элемент называется эквивалентным данной системе упругих элементов, если под действием одной и той же силы перемещения ее точки приложения совпадают.

а) Параллельное соединение упругих элементов с жесткостями с ₁ и с ₂ изображено на рис. 4 слева.

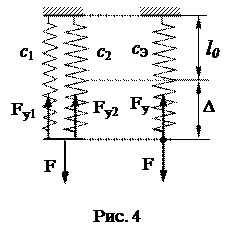
В положении равновесия сила F уравновешивается двумя силами F_у1 = с ₁ Δ и F_у2 = с ₂ Δ.

F = F_у1 + F_у2 = с ₁ Δ + с ₂ Δ = Δ(с ₁ + с ₂). (13)

У эквивалентного данной системе упругого элемента (рис. 4 справа) с жесткостью с _Э сила F уравновешивается одной силой

F = F_у = с_Э Δ. (14)

Приравняв правые части формул (13) и (14), получим: с_Э = с ₁ + с ₂.

Из этой формулы видно, что в случае параллельного соединения упругих элементов жесткость эквивалентного упругого элемента больше жесткости любого из них.

б) Последовательное соединение упругих элементов с жесткостями с ₁ и с ₂ изображено на рис. 5 слева.

Каждый из упругих элементов под действием силы F получит деформацию растяжения Δ₁ = F/ с ₁ и Δ₂ = F/ с ₂. Деформация эквивалентного упругого элемента под действием силы F равна Δ = F/ с _Э. Жесткость эквивалентного упругого элемента найдем из условия равенства деформаций: Δ = Δ₁ + Δ₂, тогда F/ с _Э = F/ с ₁ + F/ с ₂. После несложных преобразований найдем

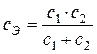(15)

Из (15) видно, что в случае последовательного соединения упругих элементов жесткость эквивалентного упругого элемента меньше жесткости любого из них.