Дифференциальное уравнение относительного движения точки

Иногда при решении задач бывает удобно рассматривать движение точки по отношению к подвижной системе отсчета. Если точка совершает сложное движение, то по теореме о сложении ускорений абсолютное ускорение есть геометрическая сумма переносного, относительного и кориолисова ускорения, т.е.

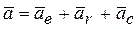. (2)

Подставив (2) в (1), получим 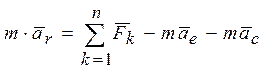(3)

Обозначим 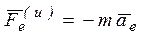, 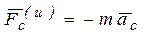. Тогда формула (3) с учетом обозначений примет вид .

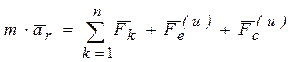Это и есть дифференциальное уравнение относительного движения точки. дифференциальное уравнение относительного движения точки ни чем не отличается от основного уравнения динамики, если к силам, действующим на точку, добавить переносную 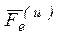и Кориолисову 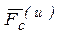силы инерции. Если переносное движение является поступательным, прямолинейным и равномерным, то 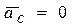и 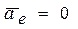. В этом случае дифференциальное уравнение относительного движения будет совпадать с основным уравнением динамики. Это говорит о том, что система отсчёта, двигающаяся относительно неподвижной поступательно, равномерно и прямолинейно, является инерциальной.