2015-05-06
878
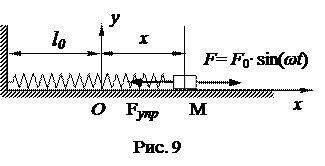
Рассмотрим движение точки (рис. 9) под действием восстанавливающей и некоторой периодической силы: F = F 0∙ sin(ωt), сопротивление среды не учитываем.
Колебания точки под действием этих сил называются вынужденными. Уравнение движения точки в этом случае имеет вид:
Разделив на массу и обозначив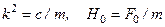 
, получим уравнение вынужденных колебаний точки без учета сопротивления среды:
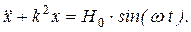(23)
Уравнение (23) является неоднородным. Его общее решение x = x 1 + x 2, где: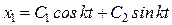 
- общее решение соответствующего однородного уравнения; x 2 – частное решение уравнения (23). Частное решение ищем в виде 
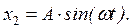Подставив это решение в уравнение (23), найдем А амплитуду вынужденных колебаний:
.
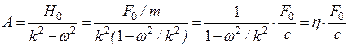Общее решение уравнения (23):
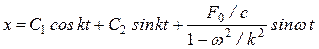. (24)
Постоянные интегрирования С 1 и С 2 можно найти из начальных условий:
при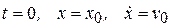 
. Коэффициент 
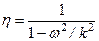- называется коэффициентом динамичности (рис. 10) и показывает, во сколько раз амплитуда
вынужденных колебаний больше статического смещения точки под действием силы F 0.
