Дифференциальные уравнения движения материальной точки

Для решения задач динамики точки будем пользоваться одной из следующих двух систем уравнений.

Уравнения в декартовых координатах. Из кинематики известно, что движение точки в прямоугольных декартовых координатах задается уравнениями:

x = f ₁(t), y = f₂(t) и z = f₃(t). (4)

Задачи динамики точки состоят в том, чтобы зная движение точки, т.е. уравнения (4), определить действующую на точку силу, или наоборот, зная действующие на точку силы, определить закон ее движения, т.е. установить уравнения (4). Следовательно, для решения задач динамики точки надо иметь уравнения, связывающие координаты x, y, z этой точки и действующую на нее силу (силы). Эти уравнения и дает второй закон динамики.

Спроектируем обе части векторного уравнения (2) на оси инерциальной системы отсчета Oxyz:

ma_x= ∑F_ix, ma_y= ∑F_iy и ma_z=∑F_iz. (5)

В уравнениях (5):

- a_x, a_y, a_z – проекции ускорения точки на оси X, Y и Z соответственно;

- ∑F_ix, ∑F_iy,∑F_iz – проекции действующей на точку силы (сил) на оси X, Y

и Z соответственно.

Учитывая, что проекции ускорения точки можно представить в виде

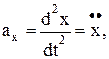
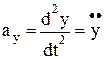и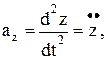

получим:

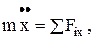
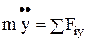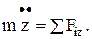и (6)

Уравнения (6) и есть искомые уравнения, т.е. дифференциальные уравнения движения материальной точки в проекциях на координатные оси.

Уравнения в проекциях на оси естественной системы отсчета. Для получения этих уравнений спроектируем векторное уравнение (1) на естественные оси координат:

- касательную (τ):

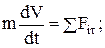(7.1)

- нормаль (n):

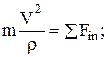(7.2)

- бинормаль (b):

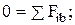(7.3)

Уравнения (7.1) – (7.3), в которых v = ds/dt, a_{n =} v²/ρ, a_τ = dv/dt и a_b = 0 представляют собой дифференциальные уравнения движения материальной точки в проекциях на естественные оси координат.