МД 2.3. Индивидуальные и локальные производные, метод Лагранжа и метод Эйлера изучения движения воздуха

Рассмотрим некоторую физическую величину q, характеризующую индивидуальную воздушную частицу (объем малых, но макроскопических размеров, в пределах которого все характеристики воздуха можно считать неизменными). Очевидно, что 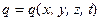, то есть, содержание физической величины в частице зависит от ее положения в пространстве и от времени. Поскольку частица движется, её координаты также являются функциями времени: 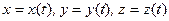. Изменение величины q со временем внутри воздушной частицы будем характеризовать производной dq / dt. Для сложной функции имеем[4]:

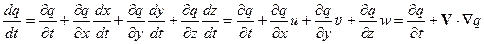, (14.7)

где использовано определение вектора скорости 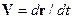(r – радиус-вектор частицы) и его проекций на оси координат. Здесь также введена операция градиента, grad или 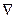, определяемая соотношениями:

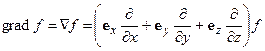. (14.8)

Производную dq/dt, характеризующую скорость изменения физической величины q в движущейся воздушной частице, называют индивидуальной или полной производной. Частную производную 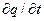, по смыслу представляющую собой изменение q в неподвижной точке пространства с координатами x, y, z, называют локальной или местной производной.

Согласно вышеприведенной формуле (14.7), изменение со временем физической величины q в точке пространства с координатами x, y, z (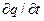) складывается из изменения со временем величины q в частице, находящейся в данный момент в рассматриваемой точке (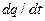), и различия в величинах q в частицах, приходящих в эту точку: ().

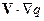Например, температура T воздуха в данной точке пространства может изменяться вследствие поглощения или испускания излучения. Этот эффект характеризуется скоростью изменения температуры в частицах воздуха в окрестности данной точки пространства – производной 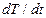. Однако та же температура может меняться из-за того, что в данную точку с воздушным течением приходят более теплые или более холодные частицы. Этот эффект характеризуется членом 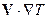. Производные 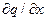называют еще пространственными или геометрическими.

В качестве другого примера рассмотрим задачу об определении ускорения частицы жидкости в ходе движения. Пусть в момент времени t положение частицы характеризовалось вектором r, а скорость – вектором V (r, t). В момент времени t+ Δ t соответственно имеем r+ Δ r, V (r+ Δ r, t+ Δ t), поскольку частица переместилась в другое положение (с точностью до членов первого порядка малости Δ r≈V (r, t)Δ t). Тогда, ограничиваясь членами первого порядка малости, находим с учетом определения частных производных[5]

,

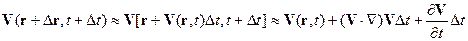откуда для ускорения окончательно получаем

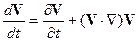
в полном соответствии с правилом (14.7). В последних двух выражениях оператор 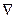рассматривается как вектор:

,

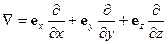а произведение 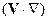действует на каждую компоненту скорости.

Если мы переходим от полной производной к частной, объектом исследования становится не воздушная частица, а свойства воздуха в различных точках пространства, то есть, поля метеорологических величин (температуры, плотности, скорости и т.п.). Такой подход к изучению течений газов и жидкостей называется методом Эйлера, а независимые переменные x, y, z, t – переменными Эйлера. Здесь, как можно догадаться, вопрос о траектории отдельных воздушных частиц не ставится.

В методе Лагранжа все величины рассматриваются как функции времени и трёх параметров, выделяющих частицу из множества остальных. Например, тремя такими параметрами могут быть координаты частицы a,b,c в некоторый момент времени t ₀: 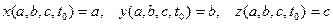. Тогда в методе Лагранжа мы находим значения физических величин частицы q (a, b, c, t) и ее координат x (a, b, c, t), y (a, b, c, t), z (a, b, c, t) в момент времени t. Изменяющиеся во времени координаты частицы определяют ее траекторию в пространстве, а зависимость от времени величины q определяет изменение содержания физической величины в частице в ходе движения.

Переменные a, b, c, t называются переменными Лагранжа [6]. В методе Лагранжа мы следим за перемещением во времени и пространстве (за траекторией) каждой отдельной частицы среды и за изменением значений физических величин, характерных для этой частицы. Очевидно, такой подход полностью соответствует концепции движения материальной точки в классической механике. Разница в том, что таких точек в случае сплошной среды очень много, и нам нужно проследить движение каждой из них. Для этого кроме времени нам необходимы переменные a, b, c, помечающие каждую частицу.

Естественно ожидать, что оба подхода к изучению движения сплошной среды должны быть эквивалентными, и должны существовать способы перехода от одних переменных к другим. В частности, разрешив функциональные зависимости x=x (a,b,c,t), y=y (a,b,c,t), z=z (a,b,c,t) относительно переменных a,b,c, получим a=a (x,y,z,t), b=b (x,y,z,t), c=c (x,y,z,t), то есть, перейдем к переменным Эйлера. При фиксированных значениях x,y,z эти зависимости позволяют определить те точки среды (частицы жидкости), которые в момент времени t приходят в данную точку пространства. Если физическая величина задана с точки зрения Лангранжа как функция q (a,b,c,t), то приведенные соотношения позволяют выразить зависимость этой величины от переменных Эйлера.

Рассмотрим теперь обратный переход от описания движения жидкости в рамках формализма Эйлера к описанию по Лагранжу. Пусть задано поле скоростей жидкости u=u (x,y,z,t), v=v (x,y,z,t), w=w (x,y,z,t). Компоненты скорости являются производными от соответствующих координат по времени при постоянных значениях параметров a,b,c, идентифицирующих частицу. Поэтому соотношения

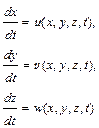
можно рассматривать как систему трех обыкновенных дифференциальных уравнений относительно x,y,z. Решив эту систему, определим x,y,z как функции времени и трех произвольных постоянных, определяемых по значениям x,y,z в некоторый момент времени t ₀. Следовательно, эти постоянные идентифицируют частицу сплошной среды и являются переменными Лагранжа. Таким образом мы определяем зависимость координат частицы жидкости от времени и от идентифицирующих ее параметров, то есть, переходим к переменным Лагранжа. Подстановка найденных решений системы уравнений в выражения для полей физических величин q (x,y,z,t) преобразует их в выражения для физических величин индивидуальных частиц жидкости, то есть, осуществляет переход к переменным Лагранжа.

В подавляющем большинстве случаев задачи о движении воздуха решаются в переменных Эйлера. Соотношение (14.7) справедливо для любой физической величины. Процедуру перехода от индивидуальных производных к локальным (и наоборот) можно осуществить, используя операторное равенство:

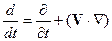. (14.9)

Преобразуем уравнение неразрывности к переменным Эйлера:

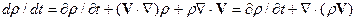. (14.10)

Следовательно

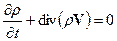. (14.11)

Это уравнение показывает, что скорость изменения плотности в заданной точке пространства определяется притоком или оттоком вещества в окрестность выбранной точки. Другими словами говорят, что скорость изменения плотности в точке определяется дивергенцией плотности потока массы .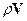

Оценки порядков величин производных, фигурирующих в уравнении неразрывности, показывают, что часто в реально наблюдаемых процессах временные производные по порядку величины заметно меньше пространственных производных. Тогда уравнение (14.11) приближенно можно записать в виде

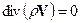. (14.12)

Наконец, иногда в задачах динамики атмосферы оказывается допустимым приближение несжимаемой жидкости. Тогда уравнение неразрывности приобретает вид

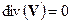. (14.13)

Приближение несжимаемой жидкости допустимо, когда изменение плотности в данной точке пространства со временем и изменение плотности при переходе от одной точки пространства к соседней незначительны по сравнению с изменением скорости в пространстве. Оказывается, такое приближение иногда вполне приемлемо при рассмотрении движений в атмосфере со скоростями, значительно меньшими скорости распространения звука. Оно совершенно не годится, когда исследуется распространение звуковых волн в воздухе.

В заключение коротко остановимся на понятии линии тока. Линия тока определяется тем, что касательная в каждой точке ее совпадает с направлением скорости в этой точке в заданный момент времени. Обратите внимание, здесь ничего не говорится о величине скорости. Следовательно, величина скорости вдоль линии тока может меняться. Исходя из определения, уравнение линии тока имеет вид 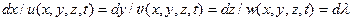(приращение элемента линии тока пропорционально скорости в заданный момент времени). Здесь 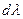- скалярный параметр. Время в приведенных уравнениях играет роль параметра, значение которого определяет разные линии тока, проходящие через точку с координатами x,y, z в разные моменты времени. Поскольку величина и направление скорости в общем случае зависят от времени, линии тока дают представление о распределении направлений скоростей движения только для одного определенного момента времени. Поэтому линии тока совпадают с траекториями частиц только в случае установившегося движения, когда скорости не зависят от времени. Приведенные выше уравнения линий тока можно также записать в виде

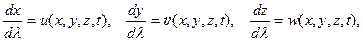
в то время как уравнения траекторий имеют вид

.

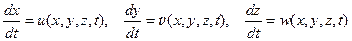Дифференциальные уравнения траекторий частиц имеют такой же вид, как и уравнения линий тока, однако время теперь не является параметром, а служит независимой переменной. Очевидно, что вектор скорости является касательной к каждой точке траектории в последовательные моменты времени, соответствующие прохождению частицы через эти точки[7].