Предварительные теоретические сведения, необходимые для решения задания 4

Бинарным отношением Ф на множествах А и В называется подмножество декартового произведения 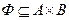. Если B=A, то Ф называется отношением на множестве A.

Бинарное отношение Ф на множестве A называется рефлексивным, если aФa для любого .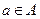

Бинарное отношение Ф на множестве A называется антирефлексивным, если для любых 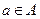, 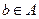для которых aФb, следует, что .

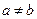Бинарное отношение Ф на множестве A называется симметричным, если из того, что выполняется aФb следует выполнение bФa.

Бинарное отношение Ф на множестве A называется антисимметричным, если из выполнения aФb и bФa следует a=b.

Бинарное отношение Ф на множестве A называется транзитивным, если из выполнения aФс и сФb следует выполнение aФb.

Рефлексивное, симметричное, транзитивное отношение Ф на множестве A называется отношением эквивалентности.

Рефлексивное, антисимметричное, транзитивное отношение Ф на множестве A называется отношением частичного порядка.

Пусть A={a₁,a₂,…,a_n}, B={b₁,b₂,…,b_m}. Матрицей [Ф] бинарного отношения Ф называется матрица, элементы 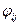которой определяются следующим образом: .

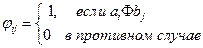Основные свойства матрицы бинарных отношений.

Отношение Ф на множестве A является

рефлексивным, если на главной диагонали матрицы [Ф] стоят единицы;

антирефлексивным, если на главной диагонали матрицы [Ф] стоят нули;

симметричным, если [Ф]=[Ф]^Т (матрица симметрична относительно главной диагонали);

антисимметричным, если в матрице [Ф] отсутствуют единицы, симметричные относительно главной диагонали;

транзитивным, если 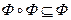. Матрица композиции 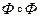равна произведению матрицы [Ф] на себя. Произведение матриц находится обычным образом. При этом полагают, что умножение совпадает с логическим умножением 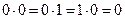, , 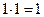а сложение совпадает с логическим сложением 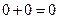, 0+1=1+0=1+1=1.