Соответствием между множествами X и Y будем называть кортеж Г=(X;Y;G). Здесь G – график соответствия, причем 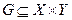 .
.
Областью определения соответствия называется 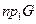 .
.
Областью значений соответствия называется 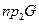 .
.
Соответствие называется всюду определенным, если 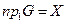 .
.
Соответствие называется сюръективным, если 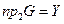 .
.
Соответствие называется функциональным, если его график не содержит пар с одинаковыми первыми и различными вторыми координатами.
Соответствие называется инъективным, если его график не содержит пар с одинаковыми вторыми и различными первыми координатами.
Соответствие называется взаимно однозначным, если оно функционально и инъективно.
Соответствие называется биекцией, если оно всюду определено, сюръективно и взаимно однозначно.
Образом множества А при данном соответствии называется множество 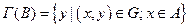 .
.
Прообразом множества B при данном соответствии называется множество 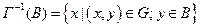 .
.
 2015-05-06
2015-05-06 779
779








