2015-05-06
12908
Наиболее просто можно определить спектр периодического сигнала. Напомним, что периодическим называется сигнал Ф (t) (рис. 2.1), удовлетворяющий следующему условию:
 |
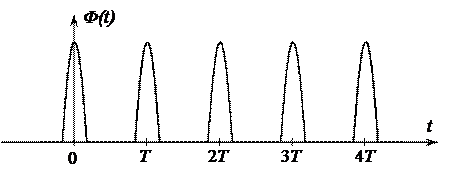Ф (t) = Ф (t + nT), где n – целое число, Т – период повторения.
Рис. 2.1. Периодический сигнал
Из курса математики известно, что всякую периодическую функцию можно представить в виде ряда Фурье:
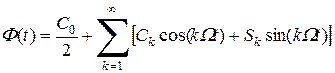, (2.1)
где
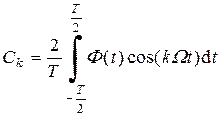, (2.2)
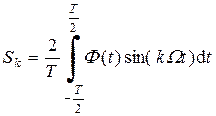, (2.3)
.
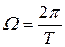Обычно используется более удобная форма записи ряда Фурье:
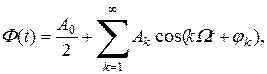(2.4)
где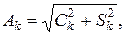 
.
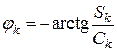Соответственно,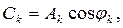 
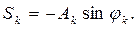
Сигнал в виде ряда Фурье удобно представить в виде спектральной диаграммы (рис. 2.2). Здесь каждая спектральная составляющая изображена вертикальной линией, высота которой пропорциональна амплитуде составляющей Ak , положение каждой составляющей на оси абсцисс определяется ее частотой kW. В случае необходимости рядом с каждой составляющей можно записывать значение фазы jk.
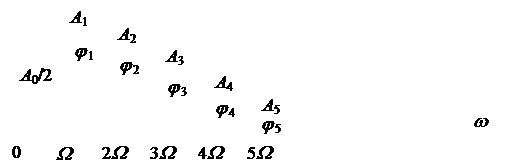
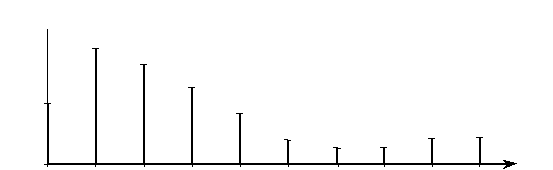
Рис. 2.2. Спектральная диаграмма периодического сигнала
Составляющая спектра с нулевой частотой называется постоянной составляющей; составляющая с частотой W (основной частотой) – первой гармоникой; составляющая с частотой 2 W – второй гармоникой и так далее.
|
|
|
Ряд Фурье может быть записан в комплексной форме. Для этого в выражении (2.4) заменим косинус его представлением по формуле Эйлера:
.
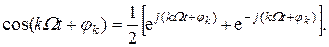В результате получим
.
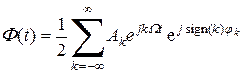Перейдем к комплексным амплитудам. Обозначим
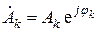– для положительных значений k,
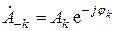– для отрицательных значений k.
В результате получим окончательное выражение для ряда Фурье в комплексной форме:
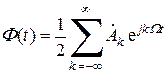(2.5)
Особенность ряда Фурье в комплексной форме состоит в том, что функция Ф (t) представлена в виде суммы составляющих вида e jkWt , причем каждому положительному значению k соответствует такое же по модулю отрицательное значение k. Линейная комбинация составляющих e jkWt и e -jkWt представляет собой гармонические функции cos(kWt) и sin(kWt), в соответствии с известными формулами Эйлера:
.
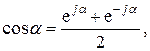
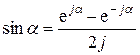Таким образом, ряд Фурье в комплексной форме также описывает разложение периодической функции на гармонические составляющие, только форма записи здесь иная.
Найдем выражение для определения комплексных амплитуд гармоник Ak. Для этого воспользуемся выражениями (2.2), (2.3):
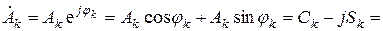
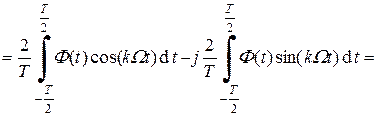
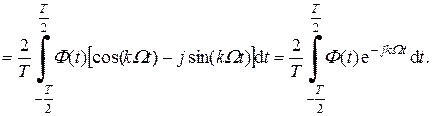(2.6)
Как будет видно из дальнейших примеров, комплексная форма ряда Фурье часто оказывается предпочтительной для вычисления спектров конкретных периодических сигналов.
Для удобства построения спектральной диаграммы вводится понятие огибающей спектра:
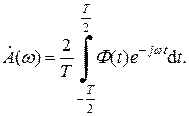(2.7)
Чтобы построить спектральную диаграмму с помощью огибающей спектра, нужно сначала с помощью формулы (2.7) найти функцию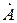 
(w), построить ее график, как показано на рис. 2.3, и затем расставить спектральные линии на расстоянии W = 2 p / Т друг от друга.
|
|
|
Рассмотрим в качестве примера построение спектральной диаграммы периодической последовательности прямоугольных импульсов, длительностью Т и и амплитудой Е (рис. 2.4).
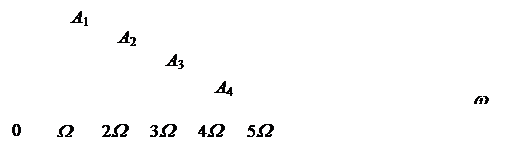
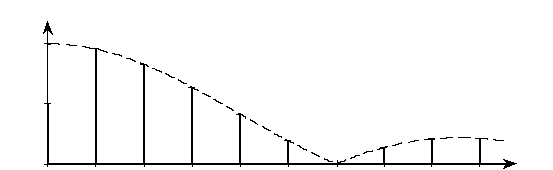
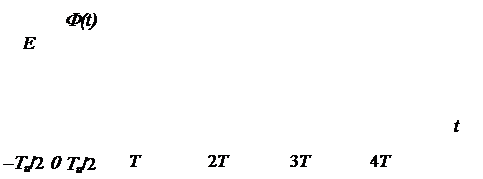Рис. 2.3. Использование огибающей спектра A(w) для построения
спектральной диаграммы
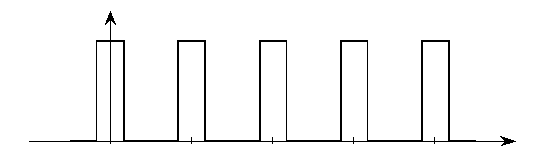
Рис. 2.4. Периодическая последовательность прямоугольных импульсов
Найдем огибающую спектра:
.
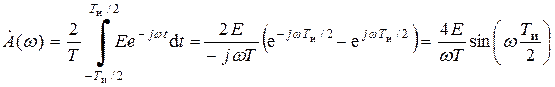Для удобства построения графика огибающей спектра полученное выше выражение для 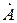(w) преобразуем к следующему виду:
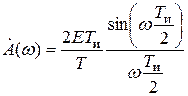. (2.8)
Огибающая спектра А (w) является вещественной функцией, ее график представлен на рис. 2.5 штриховой линией. Характерной точкой графика является значение частоты w, при котором огибающая спектра впервые обращается в нуль. Это происходит, когда аргумент синуса равен p и, следовательно, частота
w = 2 p / Т и.
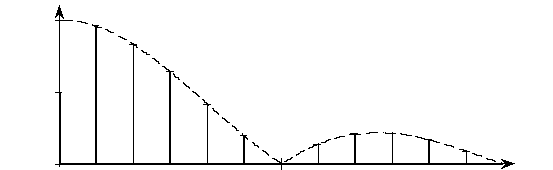
Рис. 2.5. Спектр периодической последовательности прямоугольных импульсов
Подставив в (2.8) значение частоты первой гармоники W = 2 p / Т, найдем амплитуду первой гармоники:
.
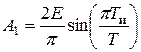Аналогично для k -й гармоники
.
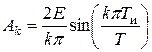Величина постоянной составляющей А 0/2 вычисляется отдельно по формуле
.
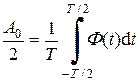В нашем случае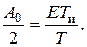 
Нетрудно видеть, что величина постоянной составляющей не равна значению огибающей спектра при w = 0, она выпадает из общей тенденции изменения амплитуд гармоник. Такая особенность спектра характерна для большинства периодических сигналов.
Необходимо отметить, что спектральное представление сигналов – не математическая абстракция, а отражение реально существующего явления. Если взять реальные гармонические сигналы с соответствующими амплитудами и фазами и сложить их, то в результате суммирования получится исходный сигнал, например, периодическая последовательность прямоугольных импульсов.
Это легче всего продемонстрировать на примере периодической последовательности прямоугольных импульсов, у которой интервал между импульсами равен длительности импульсов, т. е. Т = 2 Т и. Такой сигнал, изображенный на рис. 2.6, называется меандром. Найдем амплитуды основных гармонических составляющих меандра:
….
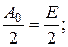
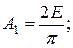
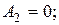
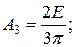
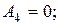
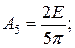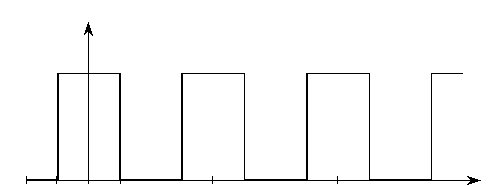
Рис. 2.6. Меандр
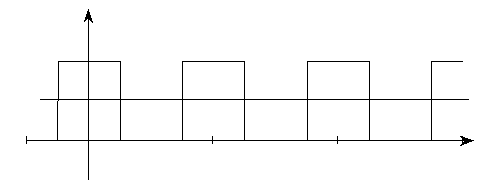
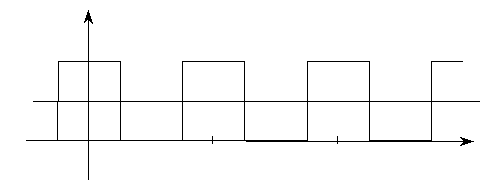
На рис. 2.7, а, б, в последовательно показаны постоянная составляющая плюс первая гармоника; сумма постоянной составляющей и первых трех гармоник; сумма постоянной составляющей и первых пяти гармоник. Хорошо видно, как с увеличением числа гармоник форма сигнала приближается к меандру.
|
|
|
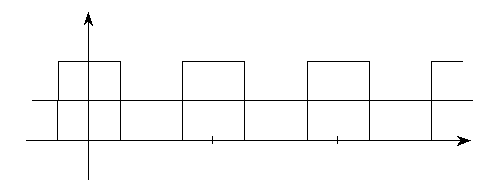
Рис. 2.7. Представление меандра суммой постоянной составляющей и первой гармоники (а),
суммой постоянной составляющей и первых трех гармоник (б), суммой постоянной
составляющей и первых пяти гармоник (в)
 |
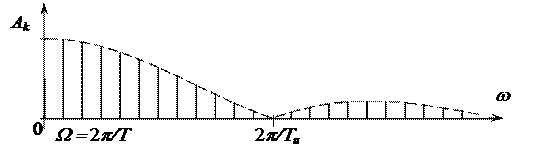Рассмотрим, как зависит характер спектра от параметров периодической последовательности импульсов. Если увеличить (или уменьшить) длительность импульсов Т и, то сожмется (или вытянется) по частоте огибающая спектра; положение спектральных линий при этом не изменится. Если же увеличивать расстояние между импульсами, т. е. период повторения Т, не изменяя размеров и формы каждого отдельного импульса, то расстояние между отдельными спектральными составляющими и их высота будут уменьшаться обратно пропорционально периоду повторения Т (рис. 2.8). Эту закономерность мы будем использовать в дальнейшем для определения спектров отдельных импульсов.
Рис. 2.8. Спектр периодического сигнала при увеличенном периоде повторения Т
