1. Даны a и b - векторы плоскости. Определить косинус угла между векторами (через скалярное произведение). Поиск скалярного произведения оформить в виде функции.
2. Дан треугольник координатами своих вершин. Определить длины сторон треугольника. Вычисление расстояния между двумя точками оформить в виде функции.
3.! Даны N точек трёхмерного пространства (заданы их названия и координаты). Указать точку, находящуюся на минимальном расстоянии от начала координат. Поиск расстояния от точки до начала координат оформить в виде функции.
- Даны три матрицы одинаковых порядков. Найти сумму максимальных элементов матриц. Генерацию матрицы оформить в виде процедуры, поиск максимального элемента - в виде функции.
- Описать функцию
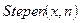 от вещественного
от вещественного 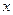 и натурального
и натурального 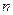 , вычисляющую (через умножение) величину
, вычисляющую (через умножение) величину 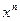 , и использовать ее для вычисления
, и использовать ее для вычисления 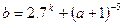 .
. - По вещественным числам
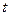 и
и 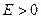 вычислите с точностью
вычислите с точностью 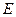 величину
величину 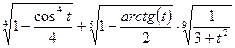 . Для вычисления корней используйте следующий ряд Тейлора:
. Для вычисления корней используйте следующий ряд Тейлора: 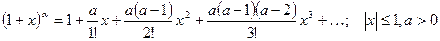 . Вычисление корня с помощью ряда оформить в виде функции.
. Вычисление корня с помощью ряда оформить в виде функции. - В квадратной матрице
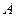
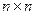 найдите строки, представляющие вектор с максимальной нормой в каждой из следующих метрик (напишите функцию для подсчета нормы вектора в указанной метрике):
найдите строки, представляющие вектор с максимальной нормой в каждой из следующих метрик (напишите функцию для подсчета нормы вектора в указанной метрике):
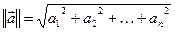
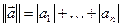
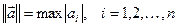 .
.
- Вычислить
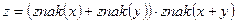 , где
, где 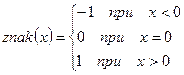 (оформить в виде функции). При решении этой задачи не использовать стандартную функцию sign.
(оформить в виде функции). При решении этой задачи не использовать стандартную функцию sign. - Даны длины
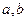 и
и 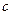 сторон некоторого треугольника. Найти медианы треугольника, сторонами которого являются медианы исходного треугольника. (Замечание: Длина медианы, проведенной к стороне
сторон некоторого треугольника. Найти медианы треугольника, сторонами которого являются медианы исходного треугольника. (Замечание: Длина медианы, проведенной к стороне 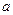 , равна
, равна 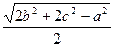 ). Вычисление медианы оформить функцией.
). Вычисление медианы оформить функцией. - Даны координаты вершин многоугольника
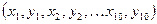 . Определите его периметр. Вычисление расстояния
. Определите его периметр. Вычисление расстояния 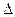 между вершинами оформите процедурой (
между вершинами оформите процедурой (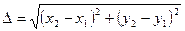 ). Рассмотрите использование процедур и функций.
). Рассмотрите использование процедур и функций. - Описать функцию
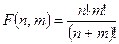 , где
, где 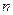 и
и 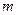 - неотрицательные целые числа. (Определить внутреннюю функцию, вычисляющую факториал.)
- неотрицательные целые числа. (Определить внутреннюю функцию, вычисляющую факториал.)
12. Даны действительные числа 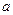 ,
, 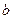 ,
, 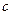 . Получить:
. Получить: 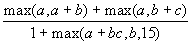 . Определение максимального из двух чисел оформить функцией.
. Определение максимального из двух чисел оформить функцией.
13. Даны действительные числа 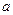 ,
, 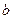 . Получить
. Получить 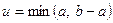 ,
, 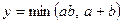 ,
, 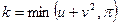 . Определение минимального из двух чисел оформить функцией.
. Определение минимального из двух чисел оформить функцией.
14.! Даны натуральные числа 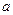 ,
, 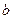 ,
, 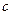 . Определить функцию
. Определить функцию 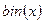 , переводящую число
, переводящую число 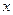 из десятичной системы счисления в двоичную. Найти
из десятичной системы счисления в двоичную. Найти 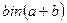 ,
, 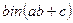 .
.
15. Даны действительные числа 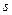 ,
, 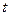 . Получить:
. Получить: 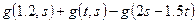 ,
, 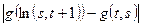 , где
, где 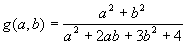 . Нахождение
. Нахождение 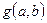 оформить функцией.
оформить функцией.
16. Даны действительные числа 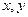 . Получить:
. Получить: 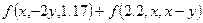 ,
, 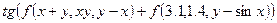 , где
, где 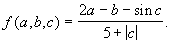
17. Даны натуральные числа 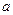 ,
, 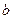 ,
, 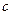 . Найти
. Найти 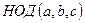 , используя формулу:
, используя формулу: 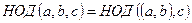 .
.
18. Даны неотрицательные целые числа 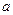 ,
, 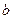 . Найти
. Найти 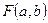 , где
, где 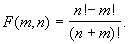 (Определить вспомогательную функцию, вычисляющую факториал).
(Определить вспомогательную функцию, вычисляющую факториал).
19. * Даны две квадратные матрицы A, B 3-го порядка. Построить таблицу функции y = cx2 + d при х меняющемся от 0 до 1 с шагом 0.1, где с = sp(A), d = sp(B). (sp(A) - след матрицы А - сумма элементов главной диагонали). Расчет следа матрицы оформить в виде функции.
20. Даны два натуральных числа 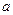 ,
, 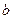 . Найти разность и произведение суммы цифр этих чисел. Вычисление суммы цифр числа оформить в виде функции.
. Найти разность и произведение суммы цифр этих чисел. Вычисление суммы цифр числа оформить в виде функции.
21.!Даны два натуральных числа 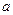 ,
, 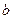 . Вычислить
. Вычислить 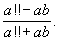 .
.
Функция 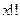 Определяется следующим образом:
Определяется следующим образом:
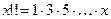 , если
, если 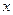 нечетно,
нечетно,
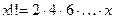 , если
, если 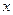 четно.
четно.
22. Даны действительные числа 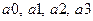 . Получить для
. Получить для 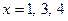 значения
значения 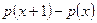 , где
, где 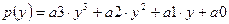 .
.
23. Даны действительные числа 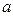 ,
, 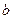 ,
, 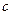 . Получить
. Получить 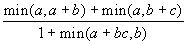 . Выбор максимума двух чисел оформить в виде функции.
. Выбор максимума двух чисел оформить в виде функции.
24. Даны действительные числа 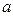 ,
, 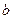 . Получить
. Получить 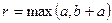 ,
, 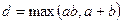 ,
, 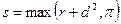 .
.
25. Даны натуральные числа 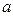 ,
, 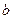 ,
, 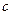 . Определить функцию
. Определить функцию 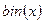 , переводящую число
, переводящую число 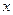 из десятичной системы счисления в двоичную. Найти двоичное представление эти чисел.
из десятичной системы счисления в двоичную. Найти двоичное представление эти чисел.
26. Даны действительные числа 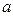 ,
, 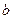 . Получить:
. Получить:
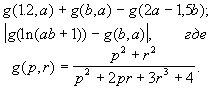
- Расчет функциональных рядов: ряды с факториалами.
Составить программу, содержащую функцию вычисления 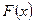 в виде бесконечного ряда с точностью
в виде бесконечного ряда с точностью 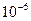 .
.
В основной программе организовать вычисление этого ряда для двух значений 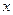 , запрашиваемых с клавиатуры, и проверку получаемых результатов путем сравнения с системной функцией
, запрашиваемых с клавиатуры, и проверку получаемых результатов путем сравнения с системной функцией 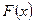 .
.
! Распечатать таблицу значений функции для 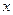 , изменяющегося в диаппазоне
, изменяющегося в диаппазоне 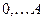 с шагом 0.1. Таблица должна содержать не более
с шагом 0.1. Таблица должна содержать не более 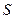 строк.
строк.
| № | 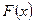 | Разложение в ряд | 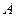 | 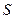 |
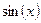 | 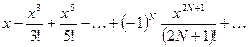 | |||
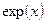 | 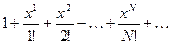 | |||
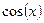 | 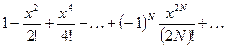 | |||
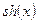 | 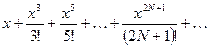 Примечание: гиперболический синус вычисляется через экспоненту как Примечание: гиперболический синус вычисляется через экспоненту как 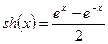 . . | |||
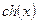 | 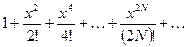 Примечание: гиперболический синус вычисляется через экспоненту как Примечание: гиперболический синус вычисляется через экспоненту как 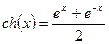 . . | |||
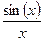 | 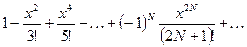 |
- Расчет функциональных рядов: разложение функции в ряд Фурье.
Составить программу с расчетом функции 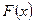 в виде ее разложения в ряд Фурье с точностью
в виде ее разложения в ряд Фурье с точностью 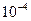 (задача гармонического анализа). Определить, какие количества членов ряда необходимо просуммировать для достижения указанной точности для значений аргумента
(задача гармонического анализа). Определить, какие количества членов ряда необходимо просуммировать для достижения указанной точности для значений аргумента 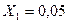 ;
; 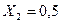 ;
; 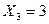 .
.
| № | 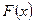 | Разложение в ряд Фурье | Диапазон аргумента |
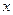 | 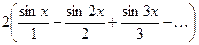 | 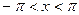 | |
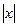 | 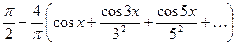 | 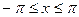 | |
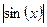 | 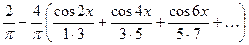 | 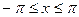 | |
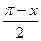 | 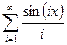 | 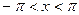 | |
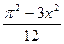 | 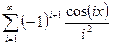 | 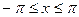 | |
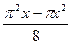 | 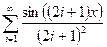 | 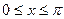 |
 2015-04-20
2015-04-20 880
880








