Задачи

1. Написать программу «Тест по таблице умножения». Сценарий: формируются 2 множителя при помощи функции RANDOM, выводится вопрос и сравнивается ответ, введенный с клавиатуры, с правильным значением. После проведения теста выводятся результаты: число заданных вопросов и число правильных ответов.
2. Вывести на экран таблицу значений функции 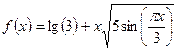. Вывод выполняется в 2 столбца: первый – значение аргумента, второй – значение функции.
3. При помощи функции RANDOM сформируйте последовательность 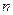случайных целых чисел. Вычислите среднее арифметическое и определите максимальное и минимальное число в последовательности.
4. Составить программу, выводящую 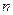членов ряда Фибоначчи (ряд Фибоначчи определяют так: ).
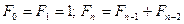5. Рассчитать сумму

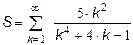
с заданной точностью e. Точность вычисления вводится с клавиатуры.

1. ! Определить все возможные двузначные числа, для которых выполняется условие: сумма квадратов цифр числа на 1 больше утроенного произведения этих цифр.
2. ! Составить программу, которая удаляет из строки все повторно встречающиеся символы. Исходная строка вводится с клавиатуры.
3. ! Разработать программу, в основе которой следующие правила. Необходимо ввести как можно больше чисел при соблюдении следующих условий: числа должны быть в диапазоне от 0 до 255; запрещается последовательно вводить числа, разность которых меньше 7. Программа заканчивает работу при первом же ошибочном вводе.
4. ! Составить программу вычисления значений 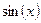в диапазоне 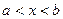с шагом 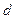. Функцию 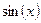описать в виде разложения в ряд Тейлора (можно отдельной функцией-подпрограммой). Количество слагаемых ряда n, границы интервала и шаг вводятся с клавиатуры.
5. ! Даны целое 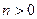и последовательность из 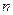вещественных чисел, среди которых есть хотя бы одно отрицательное число. Найти величину наибольшего среди отрицательных чисел этой последовательности.
6. Составьте программу вычисления значения биномиального коэффициента: .
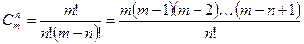7. Найдите наибольшее и наименьшее значение функции 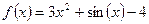, если на заданном интервале 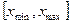аргумент изменяется с шагом .
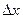8. Составьте программу вывода на экран всех простых чисел, не превосходящих заданного 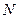. Простым называется натуральное число больше 1, имеющее только 2 делителя: 1 и само это число.
9. ! Напечатайте в убывающем порядке трехзначные числа от 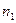до 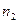, в десятичной записи которых нет одинаковых цифр.
10. ! Вычислить по схеме Горнера: 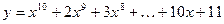. Значение 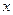ввести с клавиатуры.
11. ! Вычислить по схеме Горнера: .
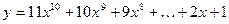12. ! Составьте программу вычисления при заданном 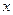значения функции вида: .
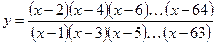13. ! Вычислить: .
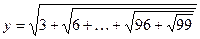14. Вычислить 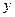- первое из чисел 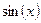, , 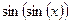, 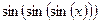…, меньшее по модулю .
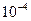15. Напишите программу для нахождения первого члена последовательности 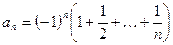, , 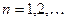который не принадлежит заданному отрезку .
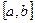16. Вычислить: 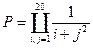и .
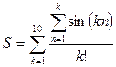17. ! Дано 200 вещественных чисел (для задания можно воспользоваться функцией RANDOM). Определить, сколько из них больше своих «соседей», т.е. предыдущего и последующего числа.
18. Для заданного значения 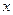вычислите 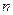-ый многочлен Чебышева, сели известны следующие соотношения: ; ; .
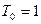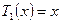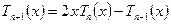19. Пусть дано 50 целых чисел, которые вводятся по одному. Получите сумму тех из них, которые:

· кратны 5;

· нечетны и отрицательны;

· меньше по абсолютному значению порядкового номера вводимого числа.

1. Составьте программу для вычисления и вывода на экран таблицы значений функции 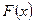. Вывод выполните в 2 столбца: первый – значение аргумента, второй – значение функции. При разработке программы следует учитывать область определения функции и в случае необходимости организовать вывод сообщения – «функция не определена».

функция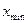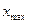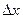
25.1.	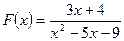0,1	1,25	0,1
25.2.	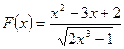	5,5	0,3
25.3.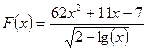

1. Необходимо составить программу расчета конечной суммы и сравнения полученного результата с контрольным значением. Число членов суммы вводится с клавиатуры с защитой от возможного неверного ввода данных.

№	вид суммы	контрольное значение

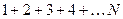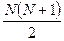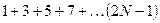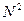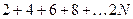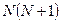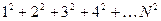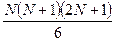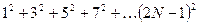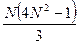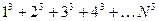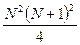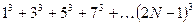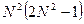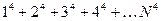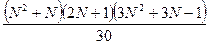1. Вычислить с точностью 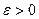значения функции:

27.1.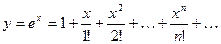

27.2.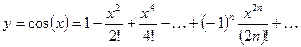

27.3. , .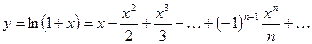

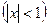27.4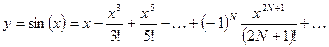

27.5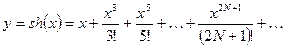

27.6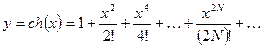

27.7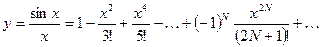

1. Расчет бесконечных сумм.

Составить программу расчета бесконечной суммы обратных степеней числового ряда. Суммирование проводить, пока очередной член ряда по модулю не станет меньше заданной точности 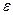. Результат сравнить с точным значением .

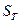№	Вид суммы		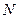Вид ряда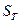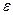

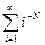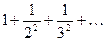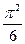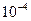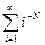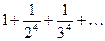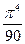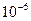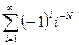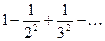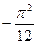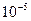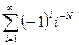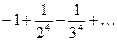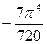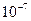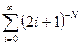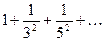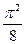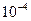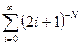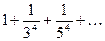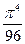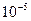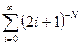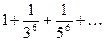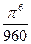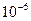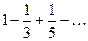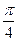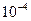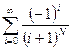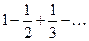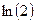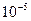1. * При заданных 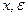вычислите сумму тех слагаемых, которые по абсолютной величине больше 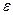: 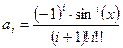, где .

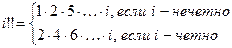1. * Разработать программу нахождения площади под кривой, заданной уравнением: 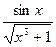, в пределах 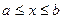, используя следующий алгоритм: В пределах 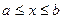строится прямоугольник, описывающий кривую (см. 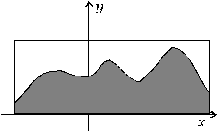рис.).

рис

Затем случайным образом ставятся точки в пределах построенного квадрата. При этом: 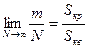, где 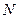- общее число точек, 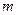- число точек, попавших в круг, 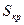- площадь под кривой, 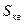- площадь квадрата.

1. Среди чисел 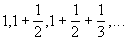найти первое число, которое больше данного числа А>0.
2. Дана последовательность 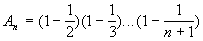и eps>0. Найти первый член последовательности 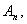для которого .
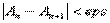3. При a > 0 задана последовательность 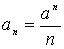. Найти при eps >0 такое n, что a_n < eps.
4. Найти произведение 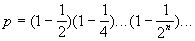Сомножители брать с точностью eps>0.
5. Найти сумму 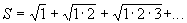, меньшую заданного числа А.
6. Вычислить сумму квадратов всех целых чисел, меньших заданного числа А.
7. Дана последовательность 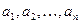вещественных чисел. Найти сумму всех элементов, больших заданного числа .
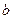8. Дана таблица целых чисел 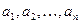. Найти количество чисел, принадлежащих отрезку .
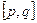9. Дана таблица целых чисел 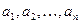и число 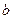. Найти минимальное значение индекса 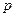, при котором .
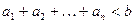10. !Дана таблица целых чисел 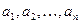. Вычислить .
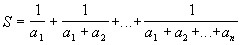11. !Дана таблица положительных чисел 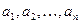. Вычислить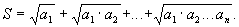

42.!Дана таблица положительных чисел 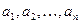. Вычислить .

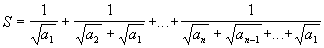1. * Составить процедуру, которая из произвольной строки, содержащей некоторый текст, выделяет все слова и печатает их в алфавитном порядке (по первой букве).
2. * Дана строка символов, состоящая из нулей, единиц и пробелов (другие символы не вводятся). Группы единиц и нулей, разделенных пробелами и не содержащие пробелов внутри себя, назовем словами. Требуется подсчитать количество слов в строке и, рассматривая слова как числа, определить количество слов, делящихся на 5 без остатка.
3. * Дана строка символов, состоящая из нулей, единиц и пробелов (другие символы не вводятся). Группы единиц и нулей, разделенных пробелами и не содержащие пробелов внутри себя, назовем словами. Требуется найти самое длинное и самое короткое слово в строке и, рассматривая эти слова как числа, определить их сумму.
4. * Дана строка символов, в которой могут встречаться цифры, пробелы, буква Е и знаки + и -. Из данной строки выделить подстроку символов, предшествующих первому пробелу. Требуется определить, является ли эта подстрока числом. Если да, то выяснить: целое или вещественное, положительное или отрицательное это число. Результат вывести на экран.
5. * Дана строка символов, содержащая некоторый текст. Разработать программу, которая определяет, является ли этот текст полиндромом, т.е. читается ли он слева направо так же, как и справа налево (например, "А роза упала на лапу Азора").
6. * В древности японский календарь использовал 60-летний цикл, состоявший из пяти 12-летних, которые обозначались цветами: зеленый, красный, желтый, белый и черный. Каждый год из числа двенадцати носил название определенного животного: крысы, коровы, тигра, зайца, дракона, змеи, лошади, овцы, обезьяны, петуха, собаки и свиньи. Составьте программу, которая вводит номер любого года нашей эры и печатает его название, если известно, что, например, 1984г. Был годом зеленой крысы и началом очередного цикла.