Задание 2 (процедуры)

1. Заданы два вектора 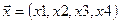, 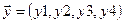. Определить угол между векторами и 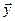по формуле: 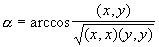Вычисление скалярного произведения оформить в виде процедуры.

2. Четыре точки заданы своими координатами 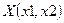, , 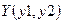, 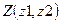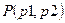. Выяснить, какие из них находятся на максимальном расстоянии друг от друга, и вывести на печать значение этого расстояния. Вычисление расстояния между двумя точками оформить в виде процедуры.

3. Четыре точки заданы своими координатами 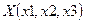, , 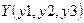, 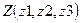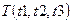. Выяснить, какие из них находятся на минимальном расстоянии друг от друга и вывести на печать значение этого расстояния. Вычисление расстояния между двумя точками оформить в виде процедуры.

4.! Три точки заданы своими координатам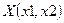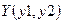и ), и 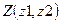. Найти и напечатать координаты точки, для которой угол между осью абсцисс и лучом, соединяющим начало координат с точкой, минимальный. Вычисления оформить в виде процедуры.

5.!По заданным вещественным числам 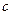и 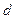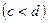вычислить 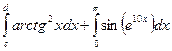. Интегралы вычилять приближенно по формуле трапеций при 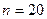для первого интеграла и при 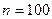для второго: 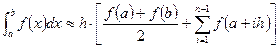, где 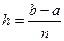. Вычисление интеграла оформить в виде процедуры или функции.

6. Задана окружность 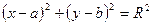и точки 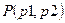, , 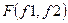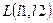. Выяснить и напечатать, сколько точек лежит внутри окружности. Проверку, лежит ли точка внутри окружности, оформить в виде процедуры.

7. * Заданы три матрицы А (первого порядка), В (второго порядка) и С (третьего порядка). Выяснить и напечатать, сколько из них являются симметрическими. (Матрица называется симметрической, если транспонированная матрица равна исходной). Транспонирование матрицы оформить в виде процедуры.

8. * Напишите процедуру, которая по заданному интервалу и функции определяет «ноль»функции с заданной точностью, используя метод деления отрезка пополам. Известно, что на границах интервала функция принимает значения, отличные по знаку. Определите «ноль» функции 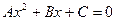для заданных .

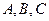9. * Заданы матрицы А и В третьего порядка. Переменной S присвоить -1, если максимальный элемент матрицы А больше максимального элемента матрицы В; 0 если максимальные элементы матрицы равны; 1, если максимальный элемент матрицы А меньше максимального элемента матрицы В. Поиск максимального элемента оформить в виде процедуры. 60710

10. Заданы два вектора 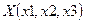, 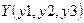и матрица А третьего порядка. Найти сумму двух векторов 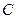и 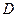, где вектор 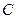есть произведение вектора 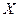на матрицу А, а вектор 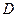- произведение вектора 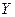на матрицу А. Вычисление произведения вектора на матрицу оформить в виде процедуры.

11. Заданы три матрицы А (третьего порядка), В (второго порядка) и С (третьего порядка). Найти максимальное из трех чисел x, y, z, где x - след матрицы А, у - след матрицы В, z - след матрицы С. (Следом матрицы называется сумма элементов главной диагонали). Вычисление следа матрицы оформить в виде процедуры.

12. Даны отрезки а, b, c и d. Для каждой тройки этих отрезков, из которой можно построить треугольник, вывести на экран площадь данного треугольника. Проверку существования треугольника оформить в виде процедуры.

13. Даны длины сторон треугольника 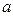, , 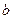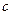. Найти медианы треугольника, сторонами которого являются медианы исходного треугольника. Для вычисления медианы проведенной к стороне 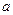, использовать формулу 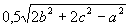Вычисление медианы оформить в виде процедуры.

14.!Даны две матрицы размером 3x3. Написать программу получения коммутатора АВ-ВА и антикоммутатора АВ+ВА этих матриц. Вычисление произведения матриц оформить в виде процедуры.

15. * Дана квадратная матрица А. Написать программу вычисления матрицы А^т*А^т*А*А, А^т - транспонированная матрица. Вычисление произведения матриц оформить в виде процедуры.

16. Даны две матрицы А и В. Написать программу, меняющую местами максимальные элементы этих матриц. Нахождение максимального элемента матрицы оформить в виде процедуры.

17.!Даны три квадратные матрицы третьего порядка. Вывести на экран ту из них, норма которой наименьшая. В качестве нормы матрицы взять максимум модулей её элементов. Нахождение нормы матрицы оформить в виде процедуры.

const n =...; {целая константа > 1}

type

num = array [1..n] of '0'..'9';

arr = array [1..40] of num;

Описать процедуру sort(x), упорядочивающую по неубыванию числа массива х следующим методом: все числа из х упорядочить по последней цифре и перенести во вспомогательный массив у; затем числа из у упорядочить по предпоследней цифре (при равенстве этих цифр сохранять упорядоченность по последней цифре) и записать их снова в массив х; далее числа из х упорядочить по третьей от конца цифре и перенести в массив у; и т. д. (Учесть, что в конце концов числа должны оказаться в х.)

19. Построить таблицу значений функции 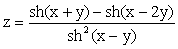, где 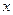меняется от 1 до 2 с шагом 0,2; 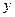меняется от 2 до 3 с шагом 0,1. Вычисление гиперболического синуса 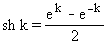оформить в виде подпрограммы (процедуры либо функции).

20. Построить таблицу значений функции 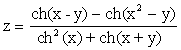, где 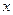меняется от 3 до 4 с шагом 0,1; 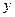меняется от 2 до 3 с шагом 0,2. Вычисление гиперболического косинуса 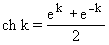оформить в виде подпрограммы (процедуры либо функции).

21. Дана целочисленная квадратная матрица размером 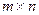. Написать процедуру, формирующую два одномерных массива. В один переслать по строкам верхний треугольник матрицы, включая элементы главной диагонали, в другой - нижний треугольник. Полученные массивы вывести на экран.

22. Даны квадратные матрицы A и B. Найти произведение этих матриц. Генерацию матриц и вывод матриц на экран оформить в виде процедур.

23. Даны координаты вершин многоугольника 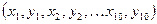. Определите его периметр. Вычисление расстояния 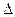между вершинами оформите процедурой (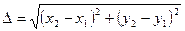). Рассмотрите использование процедур и функций.