Метод статистических испытаний (метод Монте – Карло)

К сожалению, построение аналитической модели по одной из рассмотренных выше схем удается далеко не всегда. Такая ситуация встречается при рассмотрении весьма сложных объектов или при рассмотрении новых систем, сведений о которых недостаточно для построения аналитической модели. В подобных случаях на помощь приходят так называемые численные методы. Численный метод решения математических задач при помощи моделирования случайных величин называется методом статистических испытаний или методом Монте-Карло. В основе метода лежит следующий факт: если имеется механизм генерирования (розыгрыша) значений равновероятно распределенной на отрезке [0,1] случайной величины, то легко получить случайные значения другой случайной величины, распределенной по любому заданному закону.

Генерирование значений равновероятно распределенной случайной величины обычно осуществляется с помощью так называемых псевдослучайных чисел. Сегодня практически в каждом алгоритмическом языке или пакете прикладных программ имеется стандартная процедура генерирования случайных чисел. В программе достаточно написать 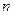: 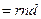и 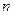будет присвоено одно из значений псевдослучайного числа. Рассмотрим механизм метода статистических испытаний.

Генерация значений непрерывной случайной величины.

Поставим задачу получить значения 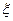случайной величины 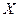, распределенной в отрезке 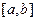с заданной плотностью .

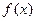При заданном законе распределения вероятность попадания случайной величины 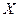в 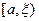находится по известно формуле

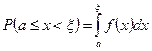(8)

Это выражение можно рассматривать в качестве уравнения относительно неизвестной 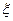. Покажем, что величина 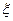, являющаяся корнем уравнения (8), имеет плотность вероятности .

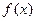Функция распределения случайной величины X

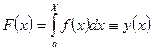
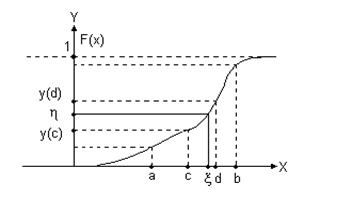монотонно возрастает от 0 до 1. Следовательно, прямая 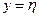(см. рис.3.5) пересекает график 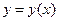в одной единственной точке, абсциссу которой принимаем за 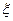. Тем самым доказано, что уравнение (8) имеет единственное решение.

Выберем произвольный интервал 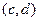, содержащийся в 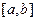. В связи с монотонностью функции 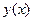, любой точке 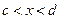соответствует ордината кривой 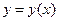, удовлетворяющая неравенству 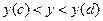. Поэтому, если 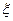принадлежит 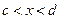, то 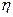принадлежит интервалу 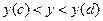, и наоборот (см. рис.3.5). Отсюда следует, что

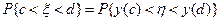(9)

Предположим, что случайная величина 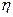на интервале (0,1) распределена равномерно. В этом случае вероятность

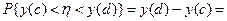
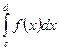(10)

Сравнивая это выражение с (1.3), получим

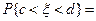
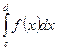. (11)

Соотношение (11) показывает, что величина 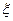имеет плотность вероятности 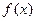. Этот факт является основанием для построения следующей схемы получения случайного значения непрерывной случайной величины 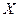, имеющей заданный закон распределения :

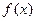1. Генерируется 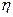- значение случайной величины, равномерно распределенной в интервале (0,1);

2. Записывается уравнение

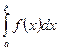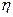= ; (12)

3. Решается уравнение (12) относительно искомой величины .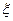

Пример 1. Розыгрыш равномерного распределения. Пусть задано распределение

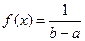для всех .

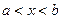Составляем уравнение

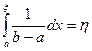
Отсюда легко получить искомый результат

.

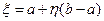Пример 2. Для случайной величины, распределенной по экспоненциальному закону 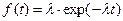для 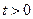, окончательная формула имеет следующий вид

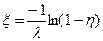(13)

Таким образом, чтобы разыграть случайную величину, распределенную по экспоненциальному закону, необходимо разыграть значение равновероятно распределенной на отрезке [0,1] величины 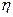, а затем подставить ее в формулу (13).

Для более сложных распределений не удается аналитически решить уравнение типа (12). Поэтому используют таблицы функций распределений. Так же разыгрывают равномерно распределенную величину 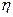, а затем по таблице ищут величину 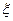, удовлетворяющую условию: .

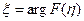Генерация значений дискретной случайной величины.

Пусть заданы значения вероятностей для некоторой дискретной случайной величины 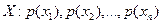. Ставится задача случайным образом выбрать одно из возможных значений 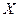, учитывая ее распределение.

Идея решения данной задачи основана на попадании случайной точки на один из интервалов, каждый из которых пропорционален величине соответствующей вероятности .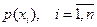

Вначале, как всегда в методе Монте-Карло, генерируется 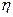- значение равновероятно распределенной в интервале (0,1) случайной величины. Затем находится искомая величина по правилу:

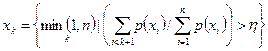(14)

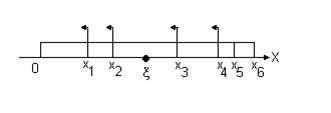
Логика этого правила заключается в следующем. Случайная точка 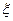попадает в один из возможных интервалов (см. рис.3.6.). Приведенное правило позволяет последовательно просматривать отношения нарастающей суммы вероятностей к их общей сумме. Считается выбранным то значение 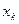, для которого впервые выполнится условие в (14).

Замечание. В целом ряде задач практики встает вопрос о случайном выборе одной из заданного множества альтернатив, каждый из которых имеет определенный вес. Его решить можно по аналогии с описанным выше методом, положив в (14) вместо вероятности нормированную величину соответствующего веса (метод рондомизированного розыгрыша).

Рассмотрим пример. Имеются четыре альтернативы 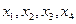с весам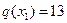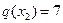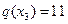и: , , и 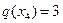. Какая альтернатива будет выбрана, если выпала h = 0,73?

Решение. В соответствии с (14) имеем:

k=1 - "13/34 = 0.382 > 0.73?" - нет;

k=2 - "20/34 = 0.588 > 0.73?" - нет;

k=3 - "31/34 = 0.912 > 0.73?" - да!

Таким образом, выбрана третья альтернатива. Если бы выпало h = 0,59, то был бы выбран тот же вариант, а вот если h = 0,27, то первый и т.д.

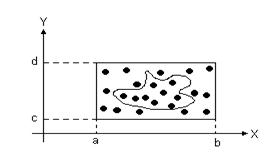
Рассмотрим пример применения метода статистических испытаний. Пусть в данный прямоугольник вписана некоторая сложная фигура (см. рис.3.7.). Требуется определить площадь вписанной фигуры.

Решение этой задачи при помощи метода статистических испытаний может происходить по следующей схеме. Реализуется механизм попадания в прямоугольник: разыгрываются случайные значения двух равновероятно распределенных случайных чисел из интервала 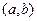и 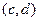, которые выступают координатами случайной точки. Всего разыгрываются 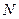точек. Из них 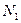попадает во вписанную фигуру, а 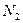- вне ее 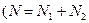. За площадь фигуры 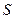принимается отношение числа точек попавших в фигуру к общему числу разыгранных точек: .

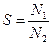Сколько розыгрышей (точек 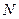) необходимо произвести, чтобы обеспечить заданную точность 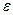? Обычно поступают следующим образом. Производится серия из достаточно представительного числа точек ( 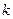штук), в результате чего получается результат 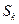. Затем серия повторяется и если

,

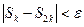то 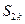принимается за конечный результат. В противном случае серии повторяются до тех пор, пока два последних результата не дадут отличие менее чем .

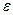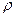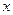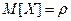Формальную оценку числа розыгрышей можно получить на основании следующих рассуждений. Пусть требуется вычислить неизвестную величину . Предположим, что имеется такая случайная величина , что и 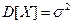. Сгенерируем 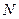значений случайной величины 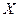. Согласно центральной предельной теореме, распределение суммы 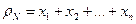приближается к нормальному закону с параметрами: математическим ожиданием 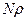и дисперсией 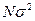. Применяя правило "трех сигм", получаем приближенное равенство

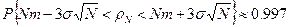
или в более компактной форме

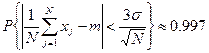(15)

Данное соотношение говорит о том, что среднее значение сгенерированной случайной величины с очень высокой вероятностью равно 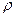. При этом ошибка не превосходит величины 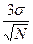, стремящейся к нулю при возрастании 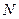. Важно подчеркнуть, что (15) позволяет оценить число розыгрышей 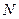, которое обеспечивает получение такой точности.