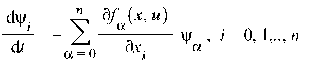 Построим еще одну систему уравнений относительно сопряженных (вспомогательных) переменных c0, c1,.., cn:
Построим еще одну систему уравнений относительно сопряженных (вспомогательных) переменных c0, c1,.., cn:
(3)
Это сопряженная система (система ДУ 1-ого порядка).
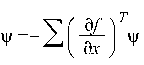 Если ввести вектор c = c0, c1,..,cn, тогда эта система будет иметь вид:
Если ввести вектор c = c0, c1,..,cn, тогда эта система будет иметь вид:
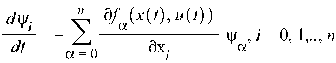 Если мы выберем некоторое допустимое управление u(t), t0 ≤ t ≤ t1, и соответствующую фазовую траекторию
Если мы выберем некоторое допустимое управление u(t), t0 ≤ t ≤ t1, и соответствующую фазовую траекторию  (t) с начальным условием
(t) с начальным условием 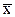 (t0)=
(t0)= 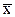 0, то из вышеприведенной системы мы получим:
0, то из вышеприведенной системы мы получим:
Получили сопряженную систему линейных однородных ДУ, которую можно решать методами теории ДУ. Тогда при любых начальных условиях ci в момент времени t0 (ci должен быть нетривиальным) эта система допускает единственное решение. Также как и решение 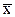 (t), решение сопряженной системы состоит из непрерывных функций ci(t), имеющих непрерывные производные.
(t), решение сопряженной системы состоит из непрерывных функций ci(t), имеющих непрерывные производные.
Объединим системы (2) и (3) одной записью, для чего определим функцию гамильтониан: H(x1,..,xn, c0,..,cn, u1,.., ur).
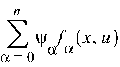
H(c,x,u) = (c,f(x,u)) =
Cистемы (2) и (3) с помощью этой функции H могут быть записаны в виде гамильтоновой системы:
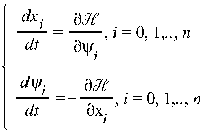
(4)
(5)
Взяв произвольное допустимое кусочно-непрерывное управление u(t), t0≤t≤t1, и начальное условие 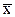 (t0)=
(t0)= 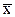 0, мы можем найти соответствующую системе (4) траекторию
0, мы можем найти соответствующую системе (4) траекторию 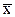 (t)={x0(t), x1(t),.., xn(t)}. После этого мы можем находить найти соответствующую системе траекторию
(t)={x0(t), x1(t),.., xn(t)}. После этого мы можем находить найти соответствующую системе траекторию 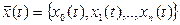 .
.
Точная верхняя грань: 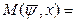 supℋ
supℋ 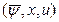
Если точная верхняя грань значений непрерывной функции Н достигается в некоторой точке области U, то 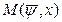 есть максимум функции Н.
есть максимум функции Н.
Теорема 1 (необходимое условие оптимальности):
Пусть u(t), t0≤t≤t1 - такое допустимое управление, что соответствующая ему траектория 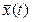 будет исходящей в момент времени t0 из точки
будет исходящей в момент времени t0 из точки 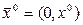 и проходящей в момент времени t1 через точку прямой П.
и проходящей в момент времени t1 через точку прямой П.
Для оптимальности управления u(t) и траектории x(t) необходимо существование такой ненулевой непрерывной вектор-функции 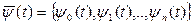 , удовлетворяющей следующим условиям:
, удовлетворяющей следующим условиям:
1.При любом t (t0≤t≤t1) функция ℋ 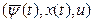 параметра
параметра 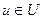 достигает в точке u=u(t) максимума.
достигает в точке u=u(t) максимума.
ℋ 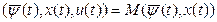
2.В конечный момент времени t1 выполняются соотношения:
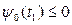
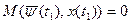
 2015-04-20
2015-04-20 274
274








