Система уравнений, описывающая движение фазовыми координатами
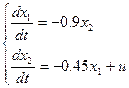 , (3)
, (3)
где
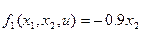 ,
, 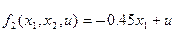 , тогда
, тогда 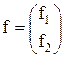 - вектор-функция правых частей дифференциальных уравнений.
- вектор-функция правых частей дифференциальных уравнений.
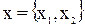 - вектор фазовых координат.
- вектор фазовых координат.
Записываем функцию Гамильтона для нашей задачи:
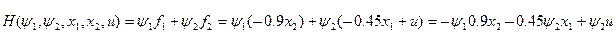
где 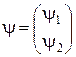 - сопряженный вектор.
- сопряженный вектор.
Для вспомогательных переменных 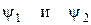 построим гамильтонову систему:
построим гамильтонову систему:
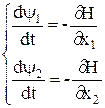 ,
, 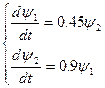
В результате получили систему линейных дифференциальных уравнений 1-ого порядка относительно 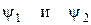 .
.
Найдем общее решение системы для 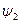 .
.
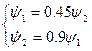
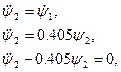
Мы получили однородное дифференциальное уравнение 2-ого порядка. Составим характеристическое уравнение:
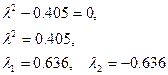
Так как корни характеристического уравнения действительные и не равны имеем:
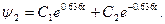
Для определения оптимального управления u определяем максимум гамильтониана Н по параметру u при фиксированных 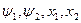 в каждый момент времени.
в каждый момент времени.
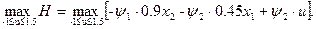
Отсюда следует, что:
при 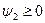 максимум функции Гамильтона достигается при u=1.5,
максимум функции Гамильтона достигается при u=1.5,
при 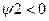 максимум функции Гамильтона достигается при u=-1, т.е.
максимум функции Гамильтона достигается при u=-1, т.е.
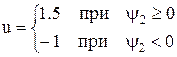
Из максимума функции Н видно, что каждое оптимальное управление u(t), где 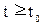
 является кусочно-постоянной функцией принимающие значение 1.5 или -1,и имеющей, не более двух интервалов знако-постоянства, так как поведение функции
является кусочно-постоянной функцией принимающие значение 1.5 или -1,и имеющей, не более двух интервалов знако-постоянства, так как поведение функции 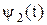 определяет экспонента, которая не более одного раза пересекает t.
определяет экспонента, которая не более одного раза пересекает t.
В конечном итоге получим:
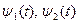 и поведение управления
и поведение управления 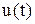 (рис.1).
(рис.1).
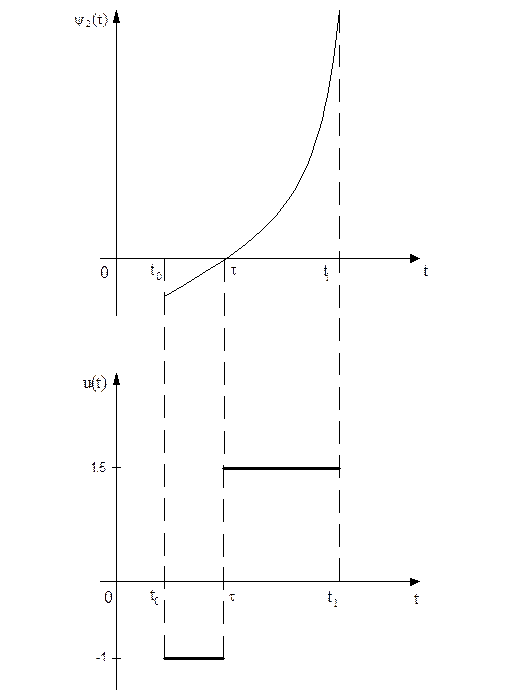
Рис.1
1.Для отрезка времени на котором 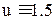 мы имеем систему ДУ:
мы имеем систему ДУ:
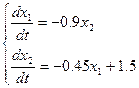
Найдем из 1-ого уравнения нашей системы:
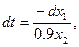
найдем из 2-ого уравнения нашей системы:
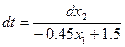 ,
,
получаем: 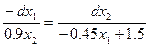 ,
,
отсюда находим:
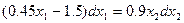 ,
,
проинтегрировав, получим общее решение:
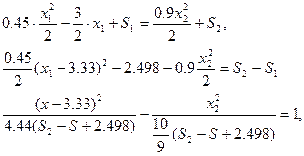
обозначим: 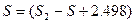 , получим:
, получим:

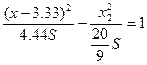 , где S принимает любое значение.
, где S принимает любое значение.
1. Пусть S>0, тогда имеем:
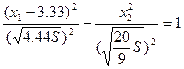 - это семейство гипербол с центром в точке (3.33;0).
- это семейство гипербол с центром в точке (3.33;0).
a= 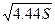 – действительная полуось.
– действительная полуось.
b= 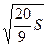 – мнимая полуось.
– мнимая полуось.
Уравнение обеих асимптот имеет вид:
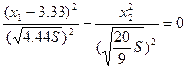 , отсюда
, отсюда
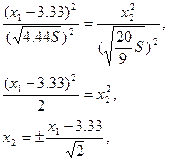
Точка пересечения асимптот O1(0,3.33).
Это семейство гипербол показано на рис.2. Для определения движения по гиперболе точки с координатами х1 и х2 берем уравнение:
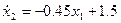
А) Если наша правая часть 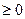 , имеем:
, имеем: 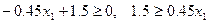 , если
, если 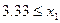 , то
, то 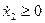 или
или 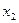 возрастает, т.е. движение вверх.
возрастает, т.е. движение вверх.
Б) Если наша производная меньше 0, имеем:
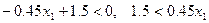 , если
, если 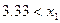 , то
, то 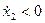 или
или 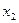 убывает, т.е. движение вниз.
убывает, т.е. движение вниз.
2. Пусть S<0. Тогда уравнение 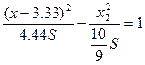 преобразуется в уравнение:
преобразуется в уравнение:
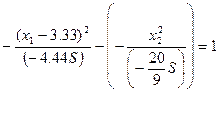
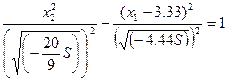 - это семейство гипербол с центром в точке (3.33;0).
- это семейство гипербол с центром в точке (3.33;0).
a= 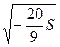 – действительная полуось.
– действительная полуось.
b= 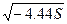 – мнимая полуось.
– мнимая полуось.
Уравнение асимптот такое же, что и в случае S>0, и имеет вид:
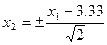 ; Т.к. гиперболы сопряженные (сопряженные гиперболы – гиперболы, уравнения которых имеют вид:
; Т.к. гиперболы сопряженные (сопряженные гиперболы – гиперболы, уравнения которых имеют вид: 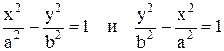 , а нашем случае:
, а нашем случае: 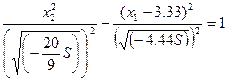 и
и 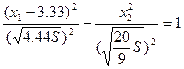 ), а сопряженные гиперболы имеют одинаковые уравнения асимптот.
), а сопряженные гиперболы имеют одинаковые уравнения асимптот.
Точка пересечения асимптот O1(0,3.33).
Это семейство гипербол показано на рис.2. Для определения движения по гиперболе точки с координатами х1 и х2 берем уравнение:
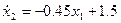
А) Если наша правая часть 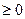 , имеем:
, имеем: 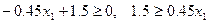 , если
, если 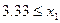 , то
, то 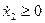 или
или 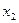 возрастает, т.е. движение вверх.
возрастает, т.е. движение вверх.
Б) Если наша производная меньше 0, имеем:
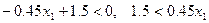 , если
, если 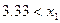 , то
, то 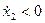 или
или 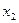 убывает, т.е. движение вниз.
убывает, т.е. движение вниз.
2. Рассмотрим интервал, на котором 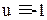 .Тогда из (3) имеем:
.Тогда из (3) имеем:
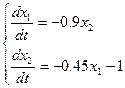 ,
,
найдем из 1-ого уравнения нашей системы:
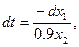
найдем из 2-ого уравнения нашей системы:
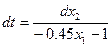 ,
,
получаем:
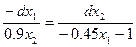
 ,
,
отсюда находим:
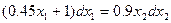 ,
,
проинтегрировав, получим:
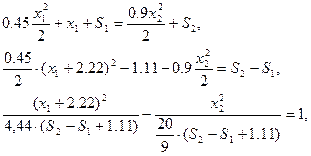
обозначим 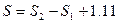 ,
,
получим:

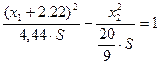
1. Пусть S>0, тогда
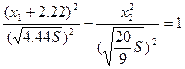 - это семейство гипербол с центром в точке (-2.22;0).
- это семейство гипербол с центром в точке (-2.22;0).
a= 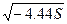 – действительная полуось,
– действительная полуось,
b= 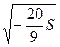 – мнимая полуось.
– мнимая полуось.
Уравнение обеих асимптот имеет вид:
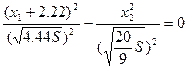 , отсюда
, отсюда
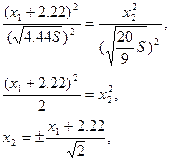
Точка пересечения асимптот O2(0,-2.22).
Это семейство гипербол показано на рис.3. Для определения движения по гиперболе точки с координатами х1 и х2 берем уравнение:
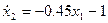
А) Если наша правая часть больше 0, имеем:
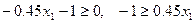 , если
, если 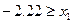 , то
, то 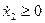 или
или 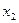 возрастает, т.е. движение вверх.
возрастает, т.е. движение вверх.
Б) Если наша левая часть меньше 0, имеем: 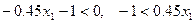 , если
, если 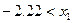 , то
, то 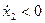 или
или 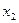 убывает, т.е. движение вниз.
убывает, т.е. движение вниз.
2. Пусть S<0. Тогда уравнение 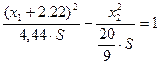 преобразуется в уравнение:
преобразуется в уравнение:
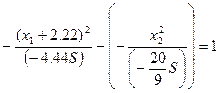
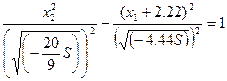 - это семейство гипербол с центром в точке (-2.22;0).
- это семейство гипербол с центром в точке (-2.22;0).
a= 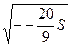 – действительная полуось,
– действительная полуось,
b= 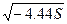 – мнимая полуось.
– мнимая полуось.
Уравнение асимптот такое же, что и в случае S>0, и имеет вид: 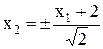
Точка пересечения асимптот O2(0,-2.22).
Это семейство гипербол показано на рис.3. Для определения движения по гиперболе точки с координатами х1 и х2 берем уравнение:
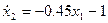
А) Если наша правая часть больше 0, имеем:
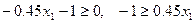 , если
, если 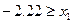 , то
, то 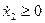 или
или 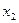 возрастает, т.е. движение вверх.
возрастает, т.е. движение вверх.
Б) Если наша левая часть меньше 0, имеем: 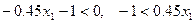 , если
, если 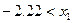 , то
, то 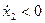 или
или 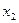 убывает, т.е. движение вниз.
убывает, т.е. движение вниз.
В начало координат приходит две траектории без переключения. Каждое оптимальное управление u(t) является кусочно-постоянной функцией принимающей -1 и 1.5. Если u(t) сначала в течении некоторого времени было равно +1.5, а затем -1, то фазовая траектория состоит из двух кусков гиперболы примыкающих друг к другу, причем второй кусок гиперболы лежит на гиперболе, которая проходит через (0;0).
Уравнение траектории, приходящее в начало координат c u=-1 без переключения имеет вид:
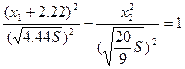 , x1=0, x2=0, отсюда имеем:
, x1=0, x2=0, отсюда имеем:
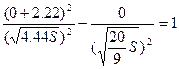 , S=1.11, следовательно:
, S=1.11, следовательно:
ОА: 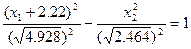 - уравнение траектории приходящее в начало координат при u=-1 без переключения.
- уравнение траектории приходящее в начало координат при u=-1 без переключения.
Уравнение траектории, приходящее в начало координат с u=1.5 без переключения имеет вид:
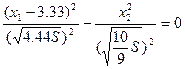 , x1=0, x2=0, отсюда имеем:
, x1=0, x2=0, отсюда имеем:
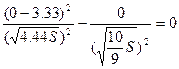 , S=2.4975, следовательно:
, S=2.4975, следовательно:
ОВ: 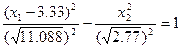 - уравнение траектории приходящее в начало координат при u=1.5 без переключения.
- уравнение траектории приходящее в начало координат при u=1.5 без переключения.
В начало координат мы можем придти по траекториям без переключения и с одним переключением. Без переключения мы приходим по ОА и ОВ, с одним переключением мы должны по траектории попасть на ОА или ОВ(рис.4)
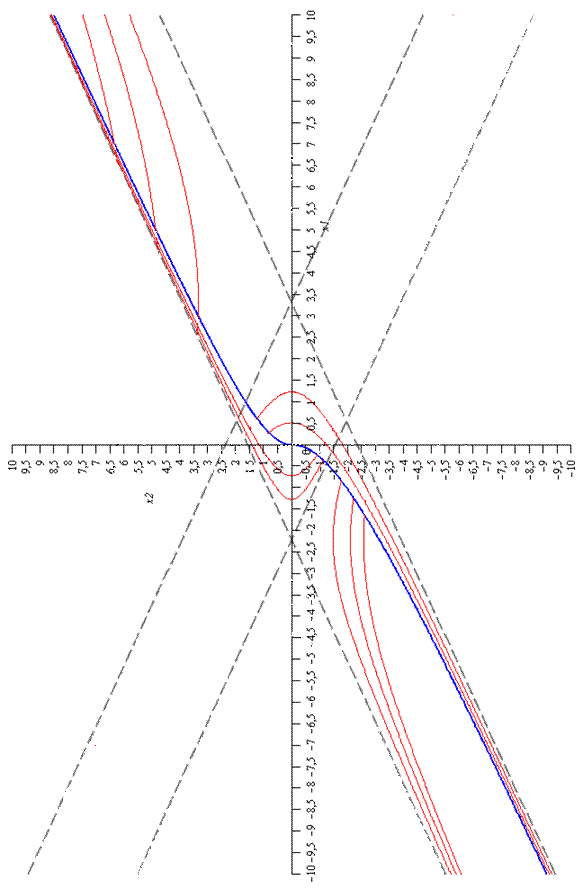
Рис.4
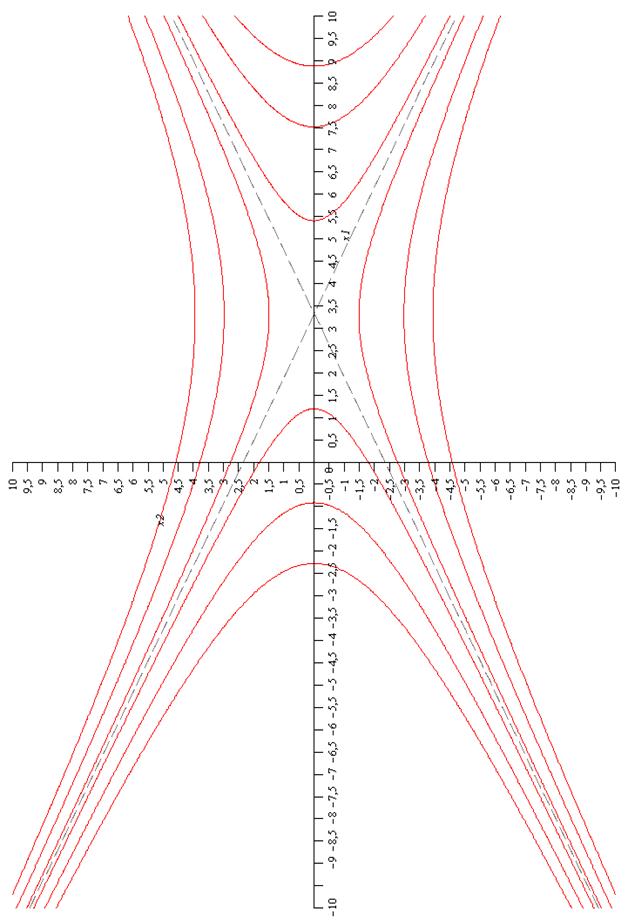
Рис.2
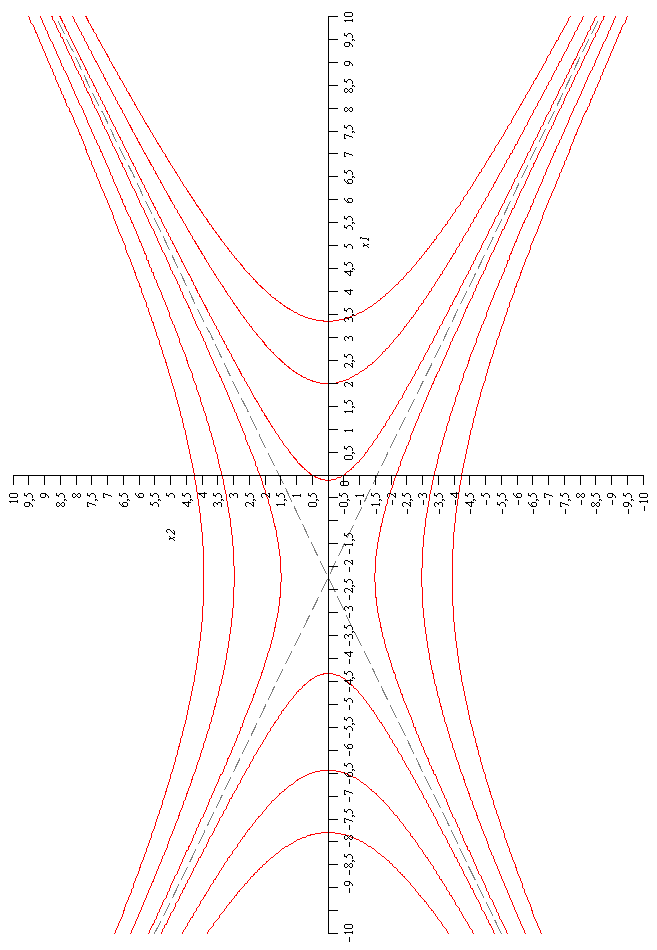
Рис.3
 2015-04-20
2015-04-20 381
381







