Пусть движение точки задано естественным способом и пусть в некоторый момент времени t точка занимала на траектории положение М, а в некоторый момент времени t1 – положение М1 (рис. 4.2). Вектор 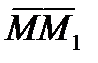 - называется вектором перемещения точки за промежуток времени
- называется вектором перемещения точки за промежуток времени 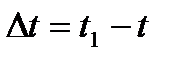 . Отношение вектора перемещения к промежутку времени, за который произошло это перемещение, называется вектором средней скорости точки, за промежуток времени
. Отношение вектора перемещения к промежутку времени, за который произошло это перемещение, называется вектором средней скорости точки, за промежуток времени 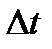 .
.
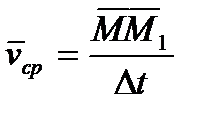 . (4.1)
. (4.1)
Вектором скорости в точке в момент времени t называется предел вектора средней скорости при стремлении промежутка 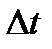 к нулю,
к нулю,
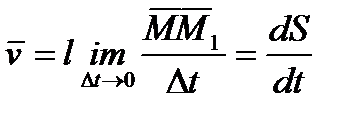 . (4.2)
. (4.2)
То есть скорость материальной точки при движении по произвольной криволинейной траектории направлена по касательной к траектории в сторону движения.
| М |
| М1 |
| v |
| vср |
Рис. 4.2
Если движение точки задано координатным способом, и движущаяся точка в момент времени t занимала положение М(x, y, z), а в момент времени t1 – положение М1(x+Dx, y+Dy, z+Dz), то вектор средней скорости 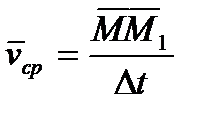 , имеет координаты
, имеет координаты 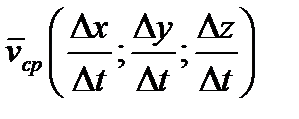 , а вектор скорости в момент времени t – координаты
, а вектор скорости в момент времени t – координаты 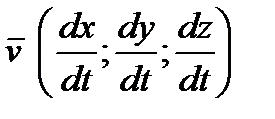 .
.
Проекции вектора скорости на оси координат: 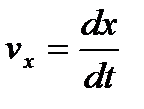 ,
, 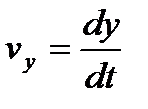 ,
, 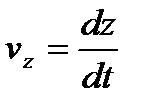 . Модуль находим по формуле
. Модуль находим по формуле
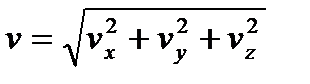 , (4.3)
, (4.3)
Косинусы углов, образуемых вектором скорости с осями координат можно найти из соотношений 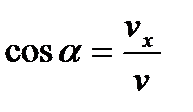 ,
, 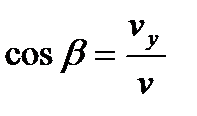 ,
, 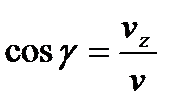 .
.
 2015-04-20
2015-04-20 505
505








