2015-04-20
9561
1. Прямолинейное движение. В этом случае траектория движения точки – прямая, причем точка движется вдоль этой прямой в одном направлении. Радиус кривизны прямой R равен бесконечности (прямую можно считать окружностью бесконечно большого радиуса). Тогда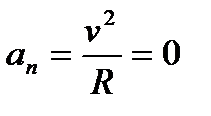 
, поэтому может изменяться только алгебраическая величина скорости точки. Это изменение полностью характеризуется касательным ускорением 
.
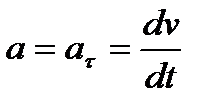2. Равномерное криволинейное движение. Так как при равномерном движении точки модуль скорости остается постоянным, то есть v = const, тогда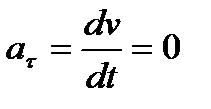 
. Вектор полного ускорения а, следовательно, направлен по главной нормали в сторону вогнутости, модуль полного ускорения равен 
.
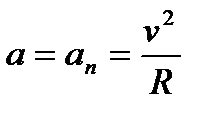3. Равномерное прямолинейное движение. В этом случае 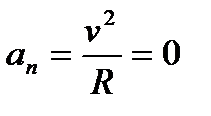и 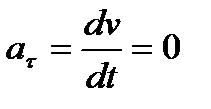, а значит а = 0. Единственный вид движения, в котором ускорение точки все время остается равным нулю, - равномерное прямолинейное движение.
4. Равнопеременное криволинейное движение. Равнопеременным называется такое криволинейное движение точки, при котором касательное ускорение остается все время величиной постоянной: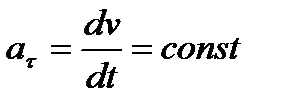 
. Если при равномерном криволинейном движении точки модуль скорости возрастает, то движение называется равноускоренным, а если убывает – равнозамедленным.
