Определение веса отдельных элементов вантовых мостов 9 страница

а) в балке устраивают временные шарниры, которые заглушают после окончания ее подвески к кабелю;

б) при уравновешенном навесе секций балку сначала не опирают на опорные части.

Но в ряде случаев больших усилий в ней не избежать, особенно для многокабельных ВС. Поэтому должны учитываться следующие особенности моделирования ВС в «0» состоянии:

– воздействие вертикальной реакции на балке в узлах крепления криволинейного кабеля;

– корректировка веса балки на участках с различным распором у ветвей для исключения перемещения промежуточных узлов на пилоне;

– задание предварительного натяжения кабеля или его ветви за счет

§ регулировки натяжения изменением длины подвесок или «нагревом» кабеля;

§ применения формальной величины сосредоточенного распора.

В начале монтажа кабель должен иметь отличное от «0» усилие предварительного натяжения для фиксации его проектного профиля.

Для многокабельных систем «0» состояние создается только один раз. На последующих этапах монтажа кабели передают балкам некомпенсированные усилия, которые следует учитывать.

Приближенные размеры сечений элементов. Определение их основывается на использовании недеформированных схем, допускающих принцип суперпозиции. Если при этом ВС достаточно жесткая, то такое решение будет «точным». Критерием жесткости ВС служит коэффициент деформативности (3.7), корректирующий усилия и прогибы (см. рис. 3.3).

Рассмотрим ВС с балкой, загруженной временной нагрузкой q по всему пролету L. Усилие распора в главном кабеле (см. рис. 3.4)

H = [(p_бал + p_пч + w_k + q) L²] / 8 f_o, (7.1)

где p_бал, p_пч, w_k – расчетные погонные нагрузки на всю ширину моста от веса балки жесткости, проезжей части и кабеля, принятые по данным подразд. 2.5; q – расчетная временная нагрузка без учета коэффициента поперечной установки (КПУ).

По условию прочности H / (cos j A_k) ≤ R_dh требуемая площадь сечения кабеля (на 2 плоскости ВС)

A_k = [(p_бал + p_пч + q) L²] / [8f_o cos a R_dh – g_k L²], (7.2)

где R_dh – прочность канатного элемента с осредненным значением R_dh =
= 800…1000 МПа; g_k – его объемный вес; a – угол наклона кабеля на вершине пилона. Аналогично подбирается сечение для усилия в подвеске
(на 2 плоскости ВС) с шагом d:

Sp = (p_бал + p_пч + q) d. (7.3)

Наибольший изгибающий момент и прогиб в четверти пролета балки при загружении l = L/2:

M_max (L/4) = q L² / 60 при L £ 150 м; (7.4)

M_max (L/4) = q L² / 100 при L ³ 500 м; (7.5)

u_max (L/4) = q^н L⁴ / (2458 EI_бал). (7.6)

По условию прочности M_max / W_бал ≤ R_бал определяется первый критерий:

I_бал (1) = (M_max h_бал) / (2 R_бал). (7.7)

По 2-му предельному состоянию определяется второй критерий:

I_бал (2) = q^н L⁴ / (2458 E [D]). (7.8)

Отсюда требуемый момент инерции балки

I_бал ³ max {I_бал (1), I_бал (2)}.

Схемы загружения имеют симметричные и несимметричные формы. Обозначение для многопролетных ВС: L_o – главный пролет, имеющий максимальную длину; L₁ – боковой пролет.

Наибольшие усилия в кабеле, пилонах и подвесках (N_к, N_p, S_p – на 2 плоскости ВС) возникают при нагружении полной нагрузкой всех пролетов моста:

(Sp + q); λ = L₁ + L_o + L₁ (схема 0),

где Sp = p^н_бал g_f + p^н_пч g_f – расчетная интенсивность от веса балочной части со всей ширины; q = q^н g_f (1 + m) n_п – расчетная временная нагрузка с учетом коэффициента полосности n_п, но без КПУ.

С участков ВМ без подвесок веса Sp необходимо перераспределить. Влиянием наклона подвесок на продольное усилие в балке пренебрегаем.

Для 1-пролетных мостов в курсовом проекте ограничиваются двумя характерными загружениями временной нагрузкой q (рис. 7.1):

1) на весь пролет – схема 1 (λ = L_o); максимальные значения: изгибающий момент M_0.5 и прогиб u_0.5;

2) на половину пролета – схема 2 (λ = 0,5L_o); экстремальные значения в четвертях проекта:

§ максимальный момент + M_0.25, минимальный – M_0.75;

§ максимальная амплитуда прогибов u_sum = |u_0.25| + |u_0.75|.

Для многопролетных ВС требуется большое число таких схем, и выбор наиболее опасных не является очевидным.

В 3-пролетных мостах максимальное формоизменение неразрезной балки жесткости возникает для трех схем нагружения q (рис. 7.2):

1) на весь главный пролет – схема 1 (λ = 0 + L_o + 0); симметричная форма дает максимальные: “–“ изгибающий момент M_0.5 (L₁) и прогиб u _0.5 (L_o);

2) на два боковые пролета – схема 2 (λ = L₁ + 0 + L₁); симметричная форма дает максимальные: “–“ опорный момент M_o (L_o), "+" момент в пролете M_0.5 (L₁) и прогиб u _0.5 (L₁);

3) на половину главного пролета – схема 3 (λ = 0 + 0,5L_o + 0); несимметричная форма, когда возникает подобие S-образного изгиба балки; экстремальные значения ориентировочно в третях пролета L_o:

§ максимальный момент + M_0.3, минимальный – M_0.7;

§ максимальная амплитуда прогибов u_sum = |u_0.3| + |u_0.8|.

На рис. 7.1, 7.2 показаны эпюры прогибов и изгибающих моментов, соответствующие всем схемам. По эпюрам строится огибающая эпюра М_ог (рис. 7.2, в). Отметим, что в каждом сечении балки жесткости действуют моменты двух знаков, изгибающих ее вверх и вниз, что характерно для ВМ. Это свойство нужно учитывать для гибридных или сталебетонных конструкций балки: их пояса по-разному воспринимают сжимающие и растягивающие усилия. В курсовом проекте при назначении сечения балки жесткости можно ограничиться максимальным по абсолютной величине значением из эпюры M_ог.

На 1-м этапе расчета требуется построение для всех перечисленных выше схем:

- расчетных балочных усилий M, N и огибающих эпюр M_ог от временной нагрузки q;

- эпюры прогибов u от нормативной временной нагрузки q_н; перевод из «расчетных» значений u выполняется делением на выражение g_f (1 + m).

для программных комплексов используются соответствующие сочетания нагрузок.

На 2-м этапе оценивается жесткость пролетного строения в целом. Сравниваются полученные при расчете величины: амплитуды u_sum для главного пролета и максимального прогиба в середине каждого пролета u_0.5 с допустимым прогибом [D]:

u_sum = u_0.25 + |u_0.75| £ [D]; (7.9)

u_0.5 £ [D]. (7.10)

Если выполняются обе проверки, то заданные при расчете программы значения A_к, I_b достаточны для обеспечения жесткости. В случае невыполнения проверки по жесткости [формула (7.9)] необходимо увеличить момент инерции балки:

I _треб = I_b (u_sum / [D]). (7.11)

г

в

б

а

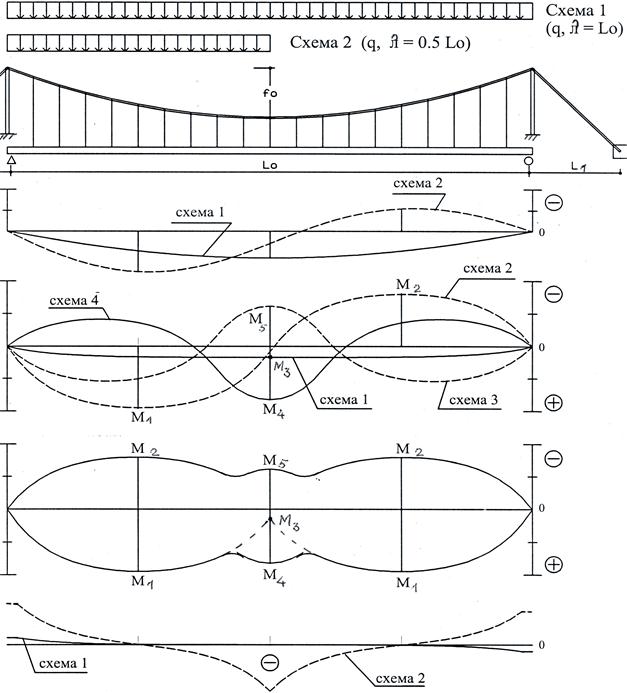
Рис. 7.1. Схемы нагружения однопролетного висячего моста и эпюры: а – прогибов u;
б – изгибающих моментов М; в – огибающая эпюра моментов М_ог; г – перерезывающих сил Q

Если же не выполняется проверка (7.10), то следует увеличить площадь сечения кабеля:

A_треб = A_к u_0.5 / [D]). (7.12)

Проверка (7.10) не выполняется обычно только при ошибке в задании A_к, как правило, u_sum >> u_0.5.

в

б

а

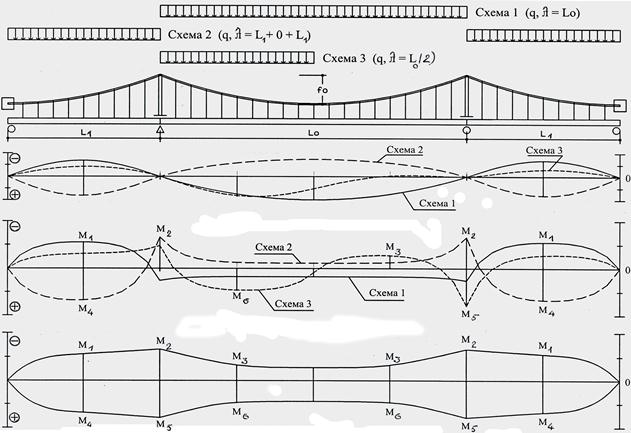
Рис. 7.2. Схемы нагружения трехпролетного висячего моста и эпюры: а – прогибов u; б – изгибающих моментов М; в – огибающая эпюра моментов М_ог

В курсовом проекте подбор сечения кабеля и подвесок выполняется только из условия прочности как для канатных элементов (см. подразд. 5.2).

Далее подобранное сечение стальной балки проверяется по условию прочности и устойчивости (см. п. 5.3.1):

– для распорных систем (N_b = 0) как для изгибаемых элементов:

M_max / (c W_b) £ R_y m;

– для безраспорных систем как для сжато-изогнутых элементов:

N_b / A_b + M_max / (c W_b) £ R_y m,

где N_b – распор, передаваемый кабелем на балку; N_b = H_p + H_q (схема 0).

Если подобранные сечения A_к, I_b превышают более чем на 50 % первоначально полученные по приближенным зависимостям, то расчет следует повторить.

Фактическое сечение балки жесткости, отвечающее всем конструктивным требованиям, должно превышать W_Б, I_Б с минимальным запасом.

Подбор сечения пилона начинается с уточнения его размеров с учетом различных форм исполнения (рис. 7.3).

		в
	а		б

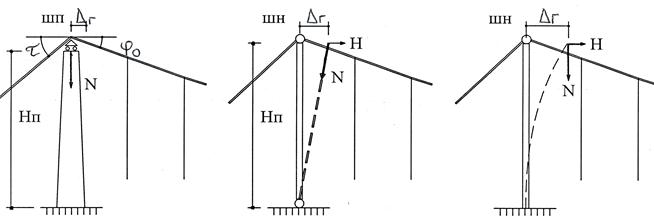
Рис. 7.3. Расчетные схемы пилона висячего моста: а – жесткого; б – полугибкого
(L₀ < 250 м); в – гибкого (L₀ > 250 м)

Жесткие пилоны, устроенные из железобетона и имеющие продольно-подвижное (ПП) опирание кабеля, рассчитываются на прочность для расчетного усилия N_p как внецентренно сжатые (см. подразд. 5.4).

Гибкие (L_o > 250 м) и полугибкие (L_o < 250 м) пилоны в курсовом проекте проверяются только на общую устойчивость в плоскости висячей «фермы». Проверять их в другой плоскости не требуется, так как эффективно работает рамная конструкция.

Для качающейся стойки полугибкого пилона коэффициент свободной длины m = 1,0, а для гибкого пилона с заделанной пятой m = 0,7.

Особенности расчета 3-пролетных висячих мостов заключаются в том, что при оценке жесткости балок не делается:

· ограничение (7.10) для выгиба ее вверх, так как прогиб в загруженном пролете (+u_0.5) всегда превышает прогиб в не загруженном (–u_0.5);

· проверка (7.9) амплитуды u_sum для сечений в разных пролетах, а только в одном пролете – главном.

Сечение балки жесткости подбирается по огибающей эпюре М_ог, у которой максимальные моменты – опорные. Для больших пролетов нужно подобрать не одно сечение (A_Б, I_Б), а два-три: в боковом пролете L₁, в опорной зоне и в главном пролете L_o. Конструктивно выполняется ступенчатое или линейное изменение сечения (рис. 7.4).

б

а

Рис. 7.4. Расчетные схемы пилона висячего моста. Изменение
изгибной жесткости EI балки: а – ступенчатое; б – линейное

Разрезные ВМ не имеют пиков опорных M_o, и балка устраивается постоянного сечения. Такую систему перестали применять для больших пролетов из-за усложнения технологии навесного монтажа. Если система несимметрично нагружена только в главном пролете (рис. 7.2, схема 3), то кабель через подвески “выравнивает” прогибы боковых пролетов: они становятся симметричными.

7.1.2. Вантовые мосты

Особенности статической работы балочно-вантовых мостов (БВМ).

· Балка жесткости обычно сжато-изогнута, что требует дополнительного обеспечения ее общей устойчивости.

· Длинные ванты могут провисать от собственного веса и снижать
жесткость системы. Это учитывается введением в расчет понижающего эффективного модуля упругости E_eff и схемы итеративно-последо­ва­тель­ного приближения.

· Главное свойство вант состоит в их односторонней работе: при сжимающих усилиях они «выключаются» из работы, а статическая схема меняется. Это явление называется конструктивной нелинейностью системы и особенно характерно для многопролетных мостов. Поэтому в расчетных моделях ванты считаются обычными сжато-растянутыми стержнями, имеющими достаточный запас растяжения за счет их предварительного натяжения.

Вантовые мосты из-за большей жесткости и прямолинейности вант, как правило, рассчитываются без учета геометрической нелинейности, что допускает построение и загружение линий влияния.

Применение пространственной расчетной модели обязательно при наличии одной плоскости вант и интенсивной работе балки жесткости на кручение.

К вантовым мостам, как к обычным статически неопределимым системам, могут применяться любые методы строительной механики, но удобнее – метод сил и смешанный метод [2, 4].

Широко используется МКЭ, имеющий большую гибкость и позволяющий моделировать практически любые конструкции. Основные недостатки МКЭ: увеличение числа неизвестных из-за приближения расчетной схемы к реальным сооружениям; затрудняется обозримость результатов.

Для большого числа вант на пилоне (n > 10) следует использовать
линейную интерполяцию их усилий, опираясь на уменьшенную сеть.

Если количество сдвоенных вант менее 10, то такую систему можно успешно считать и численно-аналитическими методами.

Регулирование внутренних усилий в элементах вантово-балочных мостов позволяет (рис. 7.5):

- выравнивать их и создавать оптимальное распределение в системе; при этом изгибающие моменты в балке уменьшаются до 1,5…2 раз;

- придавать проектное положение оси балки жесткости при эксплуатации.

Для этого балку предварительно выгибают вверх, т. е. придают ей дополнительные моменты, обратные по знаку. Это существенно уменьшает сечение балки за счет незначительного увеличения сечений для вант.

а

б

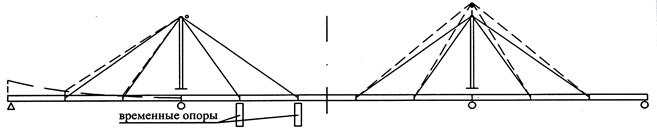
Рис. 7.5. Регулирование усилий в вантовых мостах за счет
подъема: а – опорного узла балки; б – опорной части пилона

Регулирование усилий производится, как правило, во время монтажа или перед началом эксплуатации моста. Для этого может быть использован один из следующих способов:

1) подтяжка вант при помощи домкратов или регулировочных муфт (для пешеходных мостов);

2) поддомкрачивание балки при помощи временных опор; применение монтажных пригрузов;

3) снятие временных вант, установленных при монтаже секций балки;

4) использование для железобетонных балок полигональных высокопрочных затяжек, переходящих в ванты;

5) использование температурных удлинений для гибких вант, электротермического способа – для жестких вант.

При этом конструкция узлов должна предусматривать их двойное использование – во время регулировки усилий и в процессе эксплуатации.

Предварительная вытяжка канатного элемента (КЭ) позволяет повысить приведенную осевую жесткость вант и сделать линейной зависимость между нагрузкой и перемещением, что необходимо для контроля за регулированием усилий.

В балке жесткости значения изгибающих моментов складываются из трех составляющих: от постоянной нагрузки M_p, временной нагрузки M_q и регулирования усилия M_reg. Но в курсовом проекте следует считать, что M_reg = – M_p и отдельно не учитывается.

Приближенные размеры сечений элементов устанавливаются на основании упрощения фактической работы БВМ.

Рассмотрим фрагмент вантовой системы, загруженной сосредоточенной в узле i силой F от веса одной тележки, а также временной нагрузкой q, приложенной на смежных панелях d _i и d _i+1 (рис. 7.6).

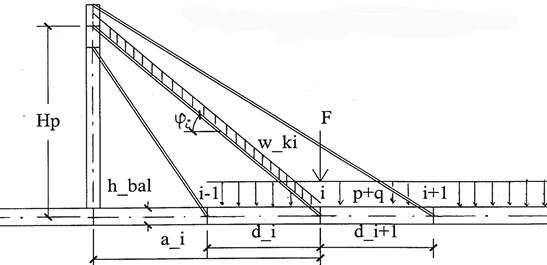
Рис. 7.6. Схема нагружения вантовой системы общего типа

Будем считать, что балка жесткости состоит из набора панелей, соединенных шарнирами в узлах крепления вант. Тогда универсальная зависимость для БВМ произвольного типа (веерная, лучевая, «арфа» и др.) дает усилие в i-й ванте:

S_i = [(p_бал + p_пч + q) + F / (30 h_бал)] [(d_i + d_i+1) / 2 sin j_i] +

+ w_ki a_i / (sin j_i cos j_i ), (7.13)

где w_ki = A_i g_k – погонная нагрузка от веса ванты g_k сечением A_i; p_бал, p_пч – расчетные постоянные нагрузки на всю ширину моста; q – расчетная временная нагрузка без учета КПУ; h_бал – высота балки; j – угол наклона ванты.

По условию прочности S_i / A_i ≤ R_dh требуемая площадь сечения i-й ванты (на все плоскости):

A_i = [(p_бал + p_пч + q) + F / (30 h_бал)] [cos j_i (d_i + d_i+1) / 2]:

: (R_dh sin j_i cos j_i – a_i g_k), (7.14)

где R_dh – прочность канатного элемента с осредненным значением R _dh =
= 400…500 Мпа; a_i – расстояние от пилона до крепления ванты к балке.

Эмпирическая формула В.К. Качурина [6] для двухпилонной лучевой (радиально-лучевой) системы с числом равных панелей n = 5–7–9 в главном пролете (п. 7.4.1):

S _i = 1,5 (p_бал + p_пч + q) (L_o – 1,06 a_i) / (n sin j_i). (7.15)

Усилия в вантах боковых пролетов, кроме оттяжек, можно принимать такими же, как и в симметричных им вантах основного пролета.

Боковая опорная ванта значительно уменьшает отклонение верха пилона. Площадь сечения опорной ванты назначается в 2–4 раза больше остальных.

Широко известна приближенная формула Н.Н. Стрелецкого для балочного изгибающего момента произвольной вантовой системы и при длине загружения l = L_o / 2:

M_max = q L 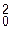/ b + (p_бал + p_пч) d / 20, (7.16)

где d_max – наибольшая длина панели между узлами опирания балки на ванты / опору; b – коэффициент, равный:

150 при 2-пилонной обычной схеме; 180 при многовантовой;

120 при 1-пилонной обычной схеме; 150 при многовантовой.

Отсюда из условия прочности M_max / W_bal ≤ R_bal определяется требуемый момент инерции и площадь сечения балки соответственно:

I_бал = (M_max h_бал) / (2 R_бал); (7.17)

A_bal = (5…6) I_бал / h_бал². (7.18)

Оптимальные параметры для вантовых мостов принимаются по данным п. 1.2.2, а также по отношениям жесткостей:

- изгибной EI_пил = (0,09…0,1) EI_бал;

- осевой для крайней и средней вант: k_v = 1,6…4,0;

- ванты и балки: с = (EA_v d ^ 3) / (EI_бал S_v) = 8…10, где S_v – длина ванты.

Схемы загружения. В отличие от висячих мостов балка жесткости у вантовых воспринимает нагрузку от собственного веса, особенно для больших панелей d. Но учитывая, что для БВМ обязательно проводится регулировка усилий (см. выше), можно ограничиться только временной нагрузкой q. При этом загружение главного пролета L_o является самым опасным.

Наибольшие усилия в вантах, пилоне и балке (N_v, N_p, N_b – на все плоскости) возникают при нагружении полной нагрузкой всех пролетов моста:

(Sp + q); λ = L₁ + L_o + L₁ (схема 0),

где Sp = p^н_бал g_f + p^н_пч g_f – расчетная интенсивность от веса балочной части со всей ширины моста; q = q^н g_f (1 + m) n _п – расчетная временная нагрузка с учетом коэффициента полосности n _п, но без КПУ.

В курсовом проекте для построения эпюр M, N, u можно ограничиться тремя схемами нагружения (рис. 7.7):

1) (q; λ = L_o) максимальные усилия в балке M_i, N_i для главного пролета;

2) (q; λ = L₁) M_i, N_i для боковых пролетов и M_о над опорным сечением;

3) (q_н; λ = L_o) экстремальные величины прогибов балки жесткости u_max.

для программных комплексов используются соответствующие
сочетания нагрузок.

На рис. 7.7 показаны балочные эпюры (u, M; схемы 1, 2) для БВМ без регулирования усилий. Видно, что опорный M_o 0, а пики M в местах крепления вант ведут к усилению сечения балок.

После этого оценивается жесткость балки: u_max £ [D]. При невыполнении условия нужно увеличить изгибную жесткость EI_б и осевые жесткости вант EA_v:

I_{b треб} = I_b (1 + (u_max – [D]) / 2 [D]), (7.19)

A_{v треб} = A_v (1 + (u_max – [D]) / 2 [D]). (7.20)

По найденным значениям усилий в вантах N_v и балке жесткости M, N определяют необходимые сечения этих элементов (см. подразд. 5.2, 5.3). При этом M_max выбирается из схем 1, 2 от нагружения q, а N – из схемы 0 от (p + q).

в

б

а

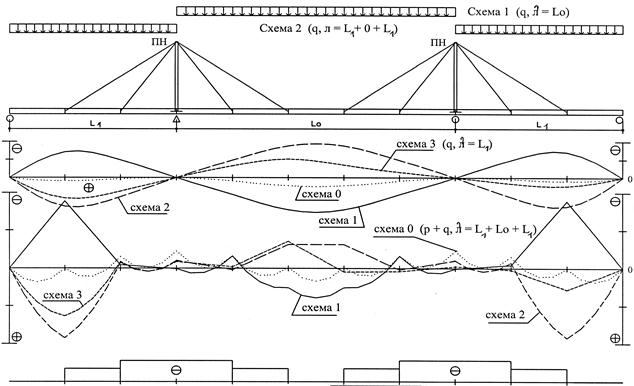
Рис. 7.7. Схемы нагружения трехпролетного вантового моста и эпюры: а – прогибов u;
б – изгибающих моментов М; в – продольных сил N в балке (схема 0)

EA_v подбирается так, чтобы u_max £ [D] (схема 3); при этом балка работает только на восприятие местной нагрузки и имеет минимальную EI_Б.

Подбор сечений стоек пилона ведется аналогично висячим мостам
(см. подразд. 5.4), но с учетом следящего эффекта из плоскости вантовой «фермы».

Для вантовых мостов характерны относительно большие длины панелей d, поэтому их следует делить двумя-тремя «информационными» точками (ИТ).

7.2. Вычислительная программа «Интэл»

Универсальная программа «Интэл» определяет напряженно-деформи-рованное состояние технических балок, подкрепленных канатными элементами в виде кабелей и вант. Алгоритм реализует метод граничных интегральных уравнений в одномерной постановке [18].

Написанная на алгоритмическом языке Fortran-90, программа предназначена для многовариантного моделирования комбинированных систем на начальном этапе проектирования, а также для курсового и дипломного проектирования как учебно-обучающая.

В частной постановке «Интэл» ориентирована на уточненное решение различных задач мостостроения.

7.2.1. Общие сведения

Программа описывает комбинированные системы (КС), состоящие из балок, пилонов и анкерных массивов, соединенных между собой канатными элементами (КЭ):

- прямолинейными оттяжками и криволинейными кабелями;

- прямолинейными / провисающими сдвоенными вантами.

Число перечисленных параметрических элементов может быть произвольным. КС строится из этого набора деталей «конструктора». При этом не требуется создавать конечно-элементную дискретизацию, так как алгоритм программы основан на интегральных зависимостях, решаемых в аналитическом виде.

В зависимости от компоновки указанных элементов формируются системы: балочная, балочно-вантовая, балочная-кабельная (висячая), много-кабельная, арочно-кабельная, висячая, усиленная вантами.

«Интэл» не учитывает такие особенности висячих систем, как

- продольное перемещения узлов кабеля;

- удлинение и наклон подвесок, их дискретность;

- локальный прогиб балки между креплением подвесок;

- упругое обжатие балок и пилонов.

Программа характеризуется:

- простотой исходных данных и наглядной топологией моделей;

- отсутствием дискретизации для элементов расчетных схем;

- параметрическим описанием сложных многокабельных систем.

Программа позволяет моделировать поэтапный монтаж многокабельных систем:

- возможность последовательного включения – исключения кабелей / вант из расчетной схемы без удаления записей в исходных данных;

- учет дополнительного воздействия на балку в ходе монтажа кабелей со стороны подвесок.

7.2.2. Функциональное описание программы

Программа «Интэл» работает под управлением операционной системы Windows-9x, но не использует диалоговые окна.

Основные функции и этапы работы программы:

- вводит исходные данные в виде текстовых файлов (*.txt);

- выводит исходную информацию в текстовые файлы (*.b_1);

- кодирует данные в формат (*.neu) для последующего МКЭ моделирования программой "FEMAP";

- вычисляет функции влияния узловых неизвестных для балок и пилонов;

- вычисляет геометрические параметры для криволинейных кабелей и сдвоенных вант;

- строит матрицы влияния отдельно для каждой балки и пилона с учетом граничных условий;

- решает систему линейных уравнений (СЛАУ) и находит основные узловые неизвестные;

- дополняет СЛАУ разрешающими уравнениями принципа Лагранжа для всех кабелей / вант в нелинейную систему;

- решает нелинейную систему методами сложной итерации и находит усилия в кабелях / вантах;

- определяет внутренние усилия в «информационных» точках (ИТ) балок;

- выводит результаты решения для нагружений в текстовый файл (*.b_2).

Программа строит эпюры в табличной и графической формах для балок и пилонов: прогибов, углов поворота сечений, изгибающих моментов и перерезывающих сил, а также усилий в подвесках.