Работа силы на криволинейном участке

Рассмотрим общий случай нахождения работы переменной силы, точка приложения которой движется по криволинейной траектории. Пусть точка М приложения переменной силы 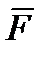движется по произвольной непрерывной кривой. Обозначим через 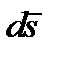вектор бесконечно малого перемещения точки М. Этот вектор направлен по касательной к кривой в ту же сторону, что и вектор скорости.

Элементарной работой переменной силы 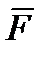на бесконечно малом перемещении 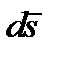называется скалярное произведение векторов 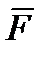и :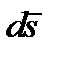

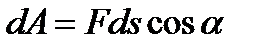, (6.11)

где a - угол между векторам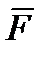и и .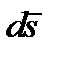

То есть элементарная работа силы равна произведению модулей векторов силы и бесконечно малого перемещения, умноженному на косинус угла между этими векторами.

Разложим вектор силы 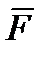на две составляющие: 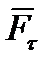- направленную по касательной к траектории – и 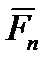– направленную по нормали (рис. 6.2). Линия действия силы 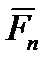перпендикулярна касательной к траектории, по которой движется точка и ее работа равна нулю, тогда:

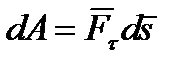. (6.12)

Для того чтобы вычислить работу переменной силы 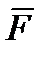на конечном участке кривой от a до b, следует вычислить интеграл от элементарной работы:

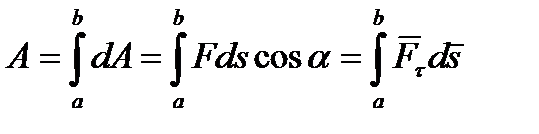. (6.13)

a

b

ds

Ft

v

Fn

F

a

Рис. 6.2

Теорема. Работа равнодействующей системы сил на некотором пути равна сумме работ составляющих сил на том же пути.

Доказательство:

Пусть точка М приложения системы сил { 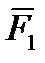, , ,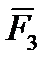… 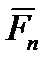} перемещается из положения М₀ в положение М₁, кроме того, пусть

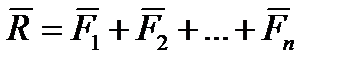, (6.14)

то есть 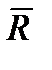– равнодействующая системы сил (рис. 6.3).

Вычислим элементарную работу силы 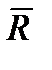. Для этого умножим равенство (6.14) скалярно на :

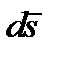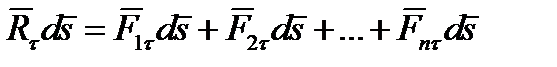, (6.15)

то есть элементарная работа равнодействующей равна сумме элементарных работ составляющих.

Представляя модули F₁, F₂, F₃,... F_n как функции s и интегрируя выражение (6.15) в соответствующих пределах, получим

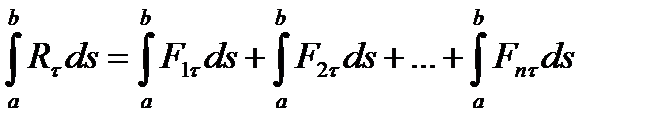. (6.16)

Поскольку 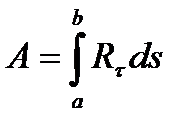, ,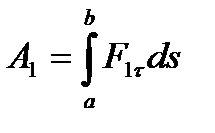..., , 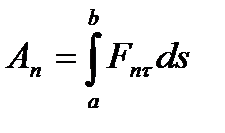окончательно имеем

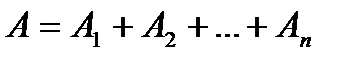, (6.17)

что и требовалось доказать.

a

b

ds

F1

Fn

F2

F3

R

M1

M0

Рис. 6.3