2015-04-20
961
Найдем работу и мощность силы, приложенной к телу, имеющему неподвижную ось вращения. Пусть к твердому телу, имеющему неподвижную ось вращения, приложена (в точке не лежащей на оси вращения) сила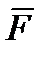 
. Траекторией точки приложения является окружность с радиусом R.
Разложим вектор 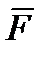на три составляющие: 
, 
, 
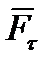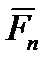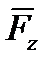(рис 7.1). Элементарная работа силы 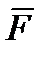будет равна
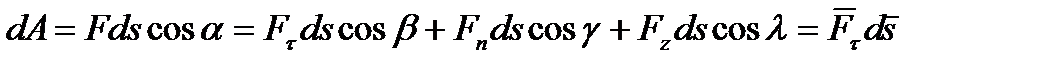, (7.5)
где a - угол между вектором силы 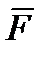и вектором перемещения 
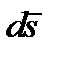, b, g, l - углы между соответствующими проекциями силы 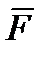и вектором .
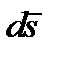Элементарные работы составляющих 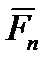и 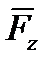равны нулю, в силу ортогональности этих составляющих перемещению 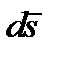. Преобразуем выражение (7.5) с учетом того, что ds=Rdj.
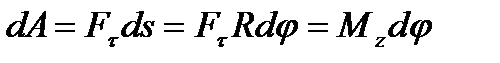. (7.6)
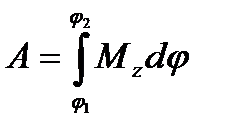, (7.7)
Если Мz = const, то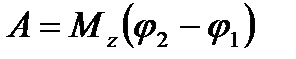 
.
Для определения мощности силы F подставим выражение элементарной работы (7.6) в формулу (7.3). Получим
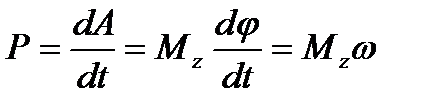, (7.8)
так как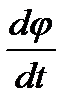 
- есть алгебраическое значение угловой скорости w вращающегося тела.
z
j
Fz
Ft
Fn
F
Рис. 7.1
