2015-04-20
313
Если дифференциальное уравнение (1) таковы что возможно найти знакоопределенную функцию v производная которой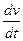 
в силу этих уравнений была бы или знакопостоянной функцией противоположного знака с vили тождественно равной O,то тривиальное решение устойчиво.
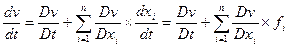
Def Если ограниченная функция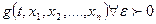 
как бы мало его не была 
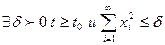, то говорят, что допускает бесконечно
Всякая независящая явно от t непрерывная функция t допускает бесконечно малый, и производная 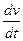, составляют в силу системы (1) является знакопеременной функцией противоположного знака, то тривиальное решение асимптотически устойчиво.
Def Назовем областью v=0 какую-нибудь область окрестности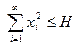 
начальная координата пространства переменных 
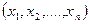ограниченного поверхностью
