В некоторых случаях, когда уравнения:
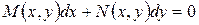
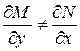
Удаётся подобрать некоторую функцию 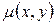 такую, что уравнение:
такую, что уравнение:
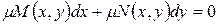
Становится уравнением в полных дифференциалах. Общее решение полученного таким образом уравнения 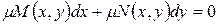 совпадает с общим решением первоначального уравнения
совпадает с общим решением первоначального уравнения 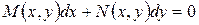 .
.
Функция 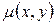 называется интегрирующим множителем уравнения
называется интегрирующим множителем уравнения 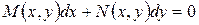 .
.
Для того, чтобы уравнение 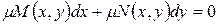 было уравнением полных дифференциалов, необходимо и достаточно, чтобы выполнялось соотношение:
было уравнением полных дифференциалов, необходимо и достаточно, чтобы выполнялось соотношение:
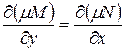
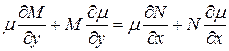
То есть
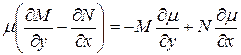
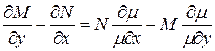
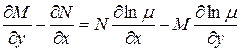 – уравнение в частных производных первого порядка с неизвестной функцией
– уравнение в частных производных первого порядка с неизвестной функцией 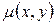 .
.
Всякая функция 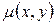 , удовлетворяющая уравнению
, удовлетворяющая уравнению 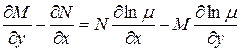 , является интегральным множителем уравнения
, является интегральным множителем уравнения 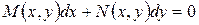 .
.
В общем случае, задача нахождения 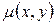 из
из 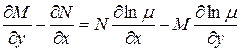 ещё труднее, чем первоначальная задача интегрирования уравнения
ещё труднее, чем первоначальная задача интегрирования уравнения 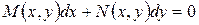 . Существуют такие частные случаи, когда удаётся найти
. Существуют такие частные случаи, когда удаётся найти 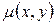 :
:
- Случай интегрирующего множителя, зависящего только от х
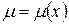
- Случай интегрирующего множителя, зависящего только от y
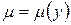
- Случай интегрирующего множителя вида
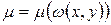
 2015-04-20
2015-04-20 1445
1445
