Системи лінійних диференціальних рівнянь з постійними коефіцієнтами та методи їх розв’язання

Def: Система д.у. наз. линейной, если она линейна относительно всех неизвестных функций и их производной. И имеет вид:

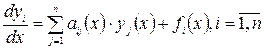
Th: Линейная комбинация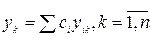

линейно независимых решений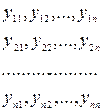

Есть общее решение линейной однородной системы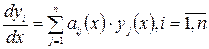

Линейные однородные системы: метод Эйлера.

Рассмотрим однородную линейную систему: 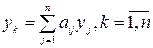, 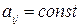(1)

Частные решение системы ищут в виде: 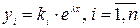(2), где 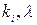- постоянные, которые надо определить так чтобы выражения (2) удовлетворяли системе (1)

Подставляяв систему (1) значения (2), сокращая на 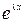и собирая коэффициенты при 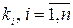получим систему алгебраических уравнений:

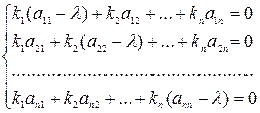(3)

(3) – система n линейных однородных уравнений относительно 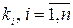. Для получения не тривиального решения системы (3) необходимо, чтобы 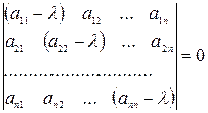(4)

Уравнение (4) наз. характеристическим уравнением системы (1), а его корни наз. корнями характеристического уравнения.

1. Все n корней характеристического уравнения действительны и различные.

Пусть эти корни будут 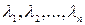. Если в (3) вместо 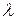поставить 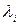- один из корней характеристического уравнения, то определитель системы (4) будет = 0, из этого следует, что система (3) имеет отличные от нуля решения: .

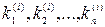Корню 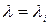соответствуют частое решение системы (1). Применяя примененное рассуждение ко всем корням 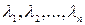характеристического уравнения получим n часных решений системы.

Полное решение системы имеет вид: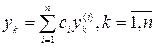

2. Корни характеристического уравнения различные, но среди них есть комплексные.

Пусть среди корней характеристического уравнения имеется два комплексных сопряженных корня: 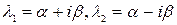им будут соответствовать решения 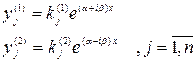– это комплексные решения.

Отделяя в них вещественные и мнимые части получим два вещественных решения.

3. Среди корней уравнения есть кратные

А) Для кратного корня 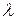есть столько линейно независимых собственных векторов какова его кратность. В этом случае ищется общее решение системы (3) соответсвующий данному 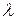зависящее от такого количества произвольных постоянных, какова кратность корня.

Б) Если 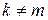, тогда находят 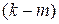- степень многочлена. Чтобы найти неизвестные коэфициенты многочлена, надо подставить решение в исходную систему, приравнять коэфициенты подобных членов в левой и правой частяхуравнений. Получится система линейных алгебраических уравнений. Найти общее решение этой системы, которое должно зависеть от 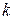- произвольных постоянных. ( 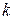-кратность).